Aprendizaje profundo I
El martes pasado concluía en Seúl la quinta y final partida de go(wéiqí en Chino) entre Lee Sedol, quizás el jugador actual más competitivo, y AlphaGo, un programa desarrollado por Google DeepMind, una subsidiaria de Google especializada en inteligencia artificial. El resultado final, 4-1, fue una victoria rotunda de la maquina sobre el ser humano.
Aunque mis habilidades con go, habiendo llegado al juego ya muy mayor, son prácticamente inexistentes, en mi familia hay varios jugadores apasionados del mismo que han dedicado, siguiendo una tradición milenaria en China, muchos años (algunos incluso décadas) al estudio de este arte (algo ahora facilitado por lasmuchas apps existentes para el iPad). Es natural, pues, que siguiésemos las cinco partidas con interés inusitado (incluyendo el parar en medio de Hyde Park en Londres para comprobar en el iPhone los últimos movimientos de cada jugador).
En comparación con el ajedrez o las damas, y a pesar de tener unas reglas a primera vista muy sencillas, go es un juego que genera muchas más combinaciones posibles de movimientos. El numero total de partidas legales de go se calcula en torno a mientras que el numero de partidas legales en ajedrez es “solo” de y en damas de un casi trivial . Esta diferencia de 50/150 órdenes de magnitud implica que el enfoque de “fuerza bruta” (literalmente, comprobar muchísimas jugadas posibles y seleccionar aquellas que maximicen el valor de la posición de las piezas en el tablero después de varias rondas de movimientos) que está en el centro del los programas tradicionales de ajedrez o de damas resulte de menos utilidad en el juego asiático.
Como consecuencia principal, un programa competitivo de go al mayor nivel tiene que diseñarse con un enfoque alternativo basado en inteligencia artificial; es decir, ha de ser un programa que de alguna manera “entienda” cómo está jugando más que simplemente comprobar todas (o casi todas) las posibilidades existentes gracias a su potencia computacional y seleccionar la mejor entre ellas.[1] Incluso entre los seres humanos, la intuición, el estilo personal y la imitación de los grandes maestros del pasado tiene mucho más importancia en go que en ajedrez; lo cual también explica porque el pico de calidad de los jugadores profesionales en go a menudo llega muy pronto en su carrera y que se puedan escribir novelas como El Maestro de Go, deYasunari Kawabata.
Y aunque muchos observadores conjeturaban que tal programa de go llegaría tarde o temprano, ha causado cierta sorpresa que haya sido en 2016. Elon Musk (el CEO de Tesla y un buen conocedor el mundo de la alta tecnología) ha citado un adelanto de diez años sobre las predicciones existentes. Tan recientemente como 2015, los mejores programas de go solo alcanzaban al nivel de un amateur sofisticado pero no podían competir con jugadores profesionales. AlphaGo, aplicando técnicas de aprendizaje profundo (en inglés, deep learning) se ha saltado esos 10 años y nos ha dejado a todos un pelín descolocados (aunque también ha habido voces escépticas sobre la generalidad de la contribución, como en este artículo de Gary Marcus).
En mi caso personal, el interés por el encuentro entre Lee Sedol y AlphaGo se reforzaba por la observación de que llevo un año trabajando en la aplicación en economía de algoritmos de aprendizaje automático (en inglés, machine learning), que incluyen los algoritmos de aprendizaje profundo como un subconjunto importante de los mismos. Y dado que este miércoles tengo que hablar sobre aprendizaje automático en economía (lo siento, no es una charla pública y no tengo transparencias que pueda circular), escribir una serie de dos entradas en NeG sobre los mismos me sirve para pulir la introducción a la misma. Dada la extensión del material a cubrir, hoy hablaré sobre el aprendizaje automático más en general y la semana que viene sobre el aprendizaje profundo que esta detrás de AlphaGo.
El aprendizaje automático es un conjunto de algoritmos diseñados para permitir que un código de ordenador aprenda sobre patrones en los datos. En vez de especificar una larga lista de atributos de los objetos a estudiar (como hacían los sistemas expertos antiguos), los algoritmos de aprendizaje automático comienzan con un simple modelo del mundo para clasificar observaciones y una serie de reglas para modificar tal modelo según el éxito del mismo. Dado que la mayoría de los ejemplos en los libros y en internet no son de economía y que los lectores de este blog podrán, llegados a este momento, estar preguntándose qué tiene todo esto que ver con nuestro campo de investigación, déjenme que les de un ejemplo. De hecho este ejemplo es el que empleo en mi propio trabajo.
Imaginémonos que disponemos de una base de datos muy amplia de la estructura financiera de empresas, como Compustat. Esta base de datos nos suministra información sobre el capital, deuda, bonos, ventas, crecimiento, etc. de un amplio abanico de empresas a lo largo de varias décadas. La cantidad de información en la misma es tremenda. El procedimiento tradicional de los economistas para analizar empíricamente tal información se ha basado en dos líneas de ataque.
Una primera línea de ataque
La primera línea de ataque, a veces llamada de forma reducida, busca especificar regresiones entre distintas variables observadas basándose en una mezcla de intuición y ligera teoría. Por ejemplo, el investigador regresa el apalancamiento de la empresa contra su tasa de crecimiento o la industria en la que opera. La idea es que, por ejemplo, si una empresa crece deprisa es probable que quiera apalancarse para aprovechar las oportunidades y financiar tal crecimiento. Este bien citado trabajo de Murray Frank y Vidhan Goyal es un ejemplo representativo de esta estrategia empírica.
Las desventajas de esta estrategia empírica son obvias. Solo por citar un problema entre muchos otros, uno nunca sabe hasta que punto los patrones documentados en los datos son espurios, producto quizás del azar, del prolongado esfuerzo del investigador de corroborar sus preconcepciones o del sesgo de publicación (es mucho más fácil publicar resultados positivos que negativos). Buena parte del esfuerzo de la econometría actual es buscar criterios de credibilidad basados en un análisis explícito de las fuentes de la identificación que permitan solventar estas dudas con un grado razonable de confianza.
Pero incluso olvidándonos de estos problemas, nos queda siempre la inquietud de que, con bases de datos amplias, incluso el investigador más perspicaz puede perderse y no descubrir patrones empíricos interesantes. Cualquiera que haya corrido regresiones complejas y presentado las mismas en público ha sufrido la experiencia de ver como un miembro de la audiencia levanta la mano y le pregunta “¿has probado x?” y pensar para uno mismo: “¿cómo no se me ha ocurrido a mi tan obvia pregunta?” Con la llegada de bases de datos masivas (en inglés, big data) este problema de mero manejo de los datos se hace cada vez más agudo, en especial en aplicaciones industriales, donde se necesitan calcular millones de regresiones con miles de potenciales regresores de manera cotidiana.
Un algoritmo de aprendizaje automático intenta explorar esta base de datos y buscar patrones empíricos robustos. En vez, por ejemplo, de probar todas y cada una de las especificaciones de regresión posibles (un problema de complejidad exponencial), podemos construir sencillos programas que encuentren relaciones en los datos y emplear las mismas para entender nuestra base de datos y predecir comportamientos futuros.
En una entrada de este blog, no puedo más que arañar la superficie de estos algoritmos, pero el libro de texto más popular sobre el tema es este de Kevin P. Murphy. Es un manual amplio, detallado y fácil de seguir. De todas maneras, y solo por ser un poco más concreto, voy a explicar la idea básica detrás de una búsqueda voraz (greedy search en inglés), un algoritmo de aprendizaje automático muy extendido y sencillo de programar.
Imaginemos que comenzamos construyendo una regresión
-regularizada del apalancamiento de una empresa contra un conjunto de variables observadas como su tasa de crecimiento, el sector en el que opera o las características de su gobernanza corporativa. La regularización nos permite penalizar aquellas especificaciones que sobre-ajustan los datos. Las variables observadas pueden ser seleccionadas aleatoriamente (si que queremos un algoritmo totalmente automático) o con unas suposiciones rápidas previas (en inglés, an educated guess). De hecho, podemos comenzar incluso con un conjunto vacío de regresores, lo que facilita la generalización del algoritmo a problemas donde tiene que ser implementado miles de veces.
Una vez estimada la primera regresión
-regularizada (o si estamos empleando un conjunto vacío, después de inicializar el programa), seleccionamos aleatoriamente una variable de las no incluidas entre los regresores para ser incluida en la segunda regresión y seleccionamos, de nuevo de manera aleatoria, una variable incluida en la primera regresión (excepto cuando comenzamos con el conjunto vacío) para ser eliminada. La selección aleatoria puede realizarse con una probabilidad positiva de no movimiento (es decir de no eliminar una variable ya existente o de no incluir una nueva variable), para que el número total de regresores sea, en si mismo, una variable aleatoria. Una vez realizado este remplazo, estimamos la nueva regresión y comprobamos una medida de ajuste a los datos. Medidas populares incluyen el nivel de la verosimilitud marginal o, en el caso de que tal verosimilitud marginal sea costosa de computar, la moda de la distribución a posteriori del modelo (este tipo de algoritmos se suelen anidar en algún tipo de Monte Carlo por Cadenas de Markov). El algoritmo puede continuar iterando en las regresiones regularizadas hasta que no se aprecien mejoras en el ajuste del modelo a los datos.
La experiencia de correr esta clase de algoritmos nos suele demostrar dos lecciones. Primero, que el ajuste va a “saltos”. En muchas iteraciones apenas avanzamos: el algoritmo parece estancado. Y, de repente, un pequeño cambio en el conjunto de regresores, trae consigo una mejora sustancial que es seguida en las siguientes iteraciones por otras mejoras importantes, antes de volverse de nuevo a estabilizar. Aquellos lectores con conocimientos de evolución reconocerán en este patrón un caso de equilibrios puntuados como los propuestos por Niles Eldredge y Stephen Jay Gould (no voy a discutir, pues no es mi campo si tales equilibrios puntuados existen o no en biología evolutiva; solo resalto que en optimización aleatoria tales equilibrios puntuados se ven todo el rato).
Segundo, que el resultado final a veces es increíblemente contra-intuitivo: los regresores que importan para ajustar los datos no son los que uno hubiese pensado. No voy a entrar en la interpretación de si estos regresores tienen o no sentido económico o de si esto ayuda a “entender” el mundo. Lo que si que conozco con 100% certeza (y aquí estoy sujeto a “non-disclosure agreements” con fuerza legal, así que he de ser deliberadamente ambiguo) es que muchas empresas han descubierto que tales regresiones aleatorias les sirven para predecir francamente bien la cantidad de unidades de un bien que necesitan almacenar en sus diferentes centros de distribución incluso cuando la regresión parece no “tener sentido” alguno. Y muchos jugadores de go pensaron que algunos de los movimientos de AlphaGo eran totalmente contra-intuitivos en tiempo real y, sin embargo, al final del día tenían mucho sentido. En otras palabras, la búsqueda aleatorizada nos hace descubrir regiones de configuraciones de la regresión o de comportamiento que no habríamos explorado de otra manera.
Una segunda línea de ataque
Mencionaba anteriormente que frente a la técnica de formas reducidas, existía una segunda línea de ataque de los economistas a los problemas empíricos (y una línea en la que yo he trabajado mucho más): el enfoque estructural. Este enfoque plantea un modelo económico explícito y, en vez de estimar regresiones, estima los parámetros que indician tal modelo (por ejemplo, los parámetros estructurales de la función de utilidad, funciones de producción o conjuntos de información). No es este el momento de repasar los argumentos a favor o en contra de este segundo enfoque. Solo apuntar rápido que los algoritmos de aprendizaje automático también tienen un papel que jugar en esta clase de enfoques, en particular en la solución de problemas de optimización de alta dimensionalidad en el corazón de los mismos (esto es, en concreto, el problema en el que estoy trabajando ahora mismo; bueno, en cuanto acabe de colgar esta entrada).
A modo de conclusión rápida
No soy, ni muchísimo menos, el primer economista en trabajar en estos temas. Susan Athey lleva años trabajando en cosas similares (aunque desde un enfoque distinto del mío). Aquí, por ejemplo, Athey discute varias de las ideas del campo y aquí, con Guido Imbens, dando unas clases magistrales sobre el tema.
En el otoño tengo programadas unas clases sobre aprendizaje automático. Si tengo tiempo de preparar unas transparencias con las que esté contento y
AlphaGo Skynet no nos ha convertido en sus esclavos, las colgaré en internet y las anunciaré aquí en NeG. Mientras tanto y en espera de la segunda entrada de esta serie el martes que viene, como dice una máquina de aprendizaje automático: “hasta la vista, baby!”
1. Los programas de ajedrez o de damas no son particularmente intrigantes desde el punto de vista de inteligencia artificial: aunque incorporan ideas interesantes de como evaluar posiciones en el tablero o de como simplificar la búsqueda de movimientos eliminando ramas del árbol de decisión de manera temprana, como reitero en el texto principal, al final del día se centran en la aplicación de fuerza bruta computacional. La victoria de DeepBlue sobre Kasparov en 1997, mientras que prueba significativa del avance en la velocidad de procesamiento, no era un cambio cualitativa en la capacidad de los ordenadores de descubrir estrategias de comportamiento óptimo. De igual manera que un ordenador puede calcular muchísimo más rápido que cualquier humano, un ordenador moderno puede evaluar muchos más movimientos de ajedrez, pero en cierto sentido no hay “mayor secreto” en ello.
{ 19 comentarios… léelos a continuación añade uno }

El martes pasado concluía en Seúl la quinta y final partida de go(wéiqí en Chino) entre Lee Sedol, quizás el jugador actual más competitivo, y AlphaGo, un programa desarrollado por Google DeepMind, una subsidiaria de Google especializada en inteligencia artificial. El resultado final, 4-1, fue una victoria rotunda de la maquina sobre el ser humano.
Aunque mis habilidades con go, habiendo llegado al juego ya muy mayor, son prácticamente inexistentes, en mi familia hay varios jugadores apasionados del mismo que han dedicado, siguiendo una tradición milenaria en China, muchos años (algunos incluso décadas) al estudio de este arte (algo ahora facilitado por lasmuchas apps existentes para el iPad). Es natural, pues, que siguiésemos las cinco partidas con interés inusitado (incluyendo el parar en medio de Hyde Park en Londres para comprobar en el iPhone los últimos movimientos de cada jugador).
En comparación con el ajedrez o las damas, y a pesar de tener unas reglas a primera vista muy sencillas, go es un juego que genera muchas más combinaciones posibles de movimientos. El numero total de partidas legales de go se calcula en torno a mientras que el numero de partidas legales en ajedrez es “solo” de y en damas de un casi trivial . Esta diferencia de 50/150 órdenes de magnitud implica que el enfoque de “fuerza bruta” (literalmente, comprobar muchísimas jugadas posibles y seleccionar aquellas que maximicen el valor de la posición de las piezas en el tablero después de varias rondas de movimientos) que está en el centro del los programas tradicionales de ajedrez o de damas resulte de menos utilidad en el juego asiático.
Como consecuencia principal, un programa competitivo de go al mayor nivel tiene que diseñarse con un enfoque alternativo basado en inteligencia artificial; es decir, ha de ser un programa que de alguna manera “entienda” cómo está jugando más que simplemente comprobar todas (o casi todas) las posibilidades existentes gracias a su potencia computacional y seleccionar la mejor entre ellas.[1] Incluso entre los seres humanos, la intuición, el estilo personal y la imitación de los grandes maestros del pasado tiene mucho más importancia en go que en ajedrez; lo cual también explica porque el pico de calidad de los jugadores profesionales en go a menudo llega muy pronto en su carrera y que se puedan escribir novelas como El Maestro de Go, deYasunari Kawabata.
Y aunque muchos observadores conjeturaban que tal programa de go llegaría tarde o temprano, ha causado cierta sorpresa que haya sido en 2016. Elon Musk (el CEO de Tesla y un buen conocedor el mundo de la alta tecnología) ha citado un adelanto de diez años sobre las predicciones existentes. Tan recientemente como 2015, los mejores programas de go solo alcanzaban al nivel de un amateur sofisticado pero no podían competir con jugadores profesionales. AlphaGo, aplicando técnicas de aprendizaje profundo (en inglés, deep learning) se ha saltado esos 10 años y nos ha dejado a todos un pelín descolocados (aunque también ha habido voces escépticas sobre la generalidad de la contribución, como en este artículo de Gary Marcus).
En mi caso personal, el interés por el encuentro entre Lee Sedol y AlphaGo se reforzaba por la observación de que llevo un año trabajando en la aplicación en economía de algoritmos de aprendizaje automático (en inglés, machine learning), que incluyen los algoritmos de aprendizaje profundo como un subconjunto importante de los mismos. Y dado que este miércoles tengo que hablar sobre aprendizaje automático en economía (lo siento, no es una charla pública y no tengo transparencias que pueda circular), escribir una serie de dos entradas en NeG sobre los mismos me sirve para pulir la introducción a la misma. Dada la extensión del material a cubrir, hoy hablaré sobre el aprendizaje automático más en general y la semana que viene sobre el aprendizaje profundo que esta detrás de AlphaGo.
El aprendizaje automático es un conjunto de algoritmos diseñados para permitir que un código de ordenador aprenda sobre patrones en los datos. En vez de especificar una larga lista de atributos de los objetos a estudiar (como hacían los sistemas expertos antiguos), los algoritmos de aprendizaje automático comienzan con un simple modelo del mundo para clasificar observaciones y una serie de reglas para modificar tal modelo según el éxito del mismo. Dado que la mayoría de los ejemplos en los libros y en internet no son de economía y que los lectores de este blog podrán, llegados a este momento, estar preguntándose qué tiene todo esto que ver con nuestro campo de investigación, déjenme que les de un ejemplo. De hecho este ejemplo es el que empleo en mi propio trabajo.
Imaginémonos que disponemos de una base de datos muy amplia de la estructura financiera de empresas, como Compustat. Esta base de datos nos suministra información sobre el capital, deuda, bonos, ventas, crecimiento, etc. de un amplio abanico de empresas a lo largo de varias décadas. La cantidad de información en la misma es tremenda. El procedimiento tradicional de los economistas para analizar empíricamente tal información se ha basado en dos líneas de ataque.
Una primera línea de ataque
La primera línea de ataque, a veces llamada de forma reducida, busca especificar regresiones entre distintas variables observadas basándose en una mezcla de intuición y ligera teoría. Por ejemplo, el investigador regresa el apalancamiento de la empresa contra su tasa de crecimiento o la industria en la que opera. La idea es que, por ejemplo, si una empresa crece deprisa es probable que quiera apalancarse para aprovechar las oportunidades y financiar tal crecimiento. Este bien citado trabajo de Murray Frank y Vidhan Goyal es un ejemplo representativo de esta estrategia empírica.
Las desventajas de esta estrategia empírica son obvias. Solo por citar un problema entre muchos otros, uno nunca sabe hasta que punto los patrones documentados en los datos son espurios, producto quizás del azar, del prolongado esfuerzo del investigador de corroborar sus preconcepciones o del sesgo de publicación (es mucho más fácil publicar resultados positivos que negativos). Buena parte del esfuerzo de la econometría actual es buscar criterios de credibilidad basados en un análisis explícito de las fuentes de la identificación que permitan solventar estas dudas con un grado razonable de confianza.
Pero incluso olvidándonos de estos problemas, nos queda siempre la inquietud de que, con bases de datos amplias, incluso el investigador más perspicaz puede perderse y no descubrir patrones empíricos interesantes. Cualquiera que haya corrido regresiones complejas y presentado las mismas en público ha sufrido la experiencia de ver como un miembro de la audiencia levanta la mano y le pregunta “¿has probado x?” y pensar para uno mismo: “¿cómo no se me ha ocurrido a mi tan obvia pregunta?” Con la llegada de bases de datos masivas (en inglés, big data) este problema de mero manejo de los datos se hace cada vez más agudo, en especial en aplicaciones industriales, donde se necesitan calcular millones de regresiones con miles de potenciales regresores de manera cotidiana.
Un algoritmo de aprendizaje automático intenta explorar esta base de datos y buscar patrones empíricos robustos. En vez, por ejemplo, de probar todas y cada una de las especificaciones de regresión posibles (un problema de complejidad exponencial), podemos construir sencillos programas que encuentren relaciones en los datos y emplear las mismas para entender nuestra base de datos y predecir comportamientos futuros.
En una entrada de este blog, no puedo más que arañar la superficie de estos algoritmos, pero el libro de texto más popular sobre el tema es este de Kevin P. Murphy. Es un manual amplio, detallado y fácil de seguir. De todas maneras, y solo por ser un poco más concreto, voy a explicar la idea básica detrás de una búsqueda voraz (greedy search en inglés), un algoritmo de aprendizaje automático muy extendido y sencillo de programar.
Imaginemos que comenzamos construyendo una regresión
Una vez estimada la primera regresión
La experiencia de correr esta clase de algoritmos nos suele demostrar dos lecciones. Primero, que el ajuste va a “saltos”. En muchas iteraciones apenas avanzamos: el algoritmo parece estancado. Y, de repente, un pequeño cambio en el conjunto de regresores, trae consigo una mejora sustancial que es seguida en las siguientes iteraciones por otras mejoras importantes, antes de volverse de nuevo a estabilizar. Aquellos lectores con conocimientos de evolución reconocerán en este patrón un caso de equilibrios puntuados como los propuestos por Niles Eldredge y Stephen Jay Gould (no voy a discutir, pues no es mi campo si tales equilibrios puntuados existen o no en biología evolutiva; solo resalto que en optimización aleatoria tales equilibrios puntuados se ven todo el rato).
Segundo, que el resultado final a veces es increíblemente contra-intuitivo: los regresores que importan para ajustar los datos no son los que uno hubiese pensado. No voy a entrar en la interpretación de si estos regresores tienen o no sentido económico o de si esto ayuda a “entender” el mundo. Lo que si que conozco con 100% certeza (y aquí estoy sujeto a “non-disclosure agreements” con fuerza legal, así que he de ser deliberadamente ambiguo) es que muchas empresas han descubierto que tales regresiones aleatorias les sirven para predecir francamente bien la cantidad de unidades de un bien que necesitan almacenar en sus diferentes centros de distribución incluso cuando la regresión parece no “tener sentido” alguno. Y muchos jugadores de go pensaron que algunos de los movimientos de AlphaGo eran totalmente contra-intuitivos en tiempo real y, sin embargo, al final del día tenían mucho sentido. En otras palabras, la búsqueda aleatorizada nos hace descubrir regiones de configuraciones de la regresión o de comportamiento que no habríamos explorado de otra manera.
Una segunda línea de ataque
Mencionaba anteriormente que frente a la técnica de formas reducidas, existía una segunda línea de ataque de los economistas a los problemas empíricos (y una línea en la que yo he trabajado mucho más): el enfoque estructural. Este enfoque plantea un modelo económico explícito y, en vez de estimar regresiones, estima los parámetros que indician tal modelo (por ejemplo, los parámetros estructurales de la función de utilidad, funciones de producción o conjuntos de información). No es este el momento de repasar los argumentos a favor o en contra de este segundo enfoque. Solo apuntar rápido que los algoritmos de aprendizaje automático también tienen un papel que jugar en esta clase de enfoques, en particular en la solución de problemas de optimización de alta dimensionalidad en el corazón de los mismos (esto es, en concreto, el problema en el que estoy trabajando ahora mismo; bueno, en cuanto acabe de colgar esta entrada).
A modo de conclusión rápida
No soy, ni muchísimo menos, el primer economista en trabajar en estos temas. Susan Athey lleva años trabajando en cosas similares (aunque desde un enfoque distinto del mío). Aquí, por ejemplo, Athey discute varias de las ideas del campo y aquí, con Guido Imbens, dando unas clases magistrales sobre el tema.
En el otoño tengo programadas unas clases sobre aprendizaje automático. Si tengo tiempo de preparar unas transparencias con las que esté contento y
AlphaGo Skynet no nos ha convertido en sus esclavos, las colgaré en internet y las anunciaré aquí en NeG. Mientras tanto y en espera de la segunda entrada de esta serie el martes que viene, como dice una máquina de aprendizaje automático: “hasta la vista, baby!”
1. Los programas de ajedrez o de damas no son particularmente intrigantes desde el punto de vista de inteligencia artificial: aunque incorporan ideas interesantes de como evaluar posiciones en el tablero o de como simplificar la búsqueda de movimientos eliminando ramas del árbol de decisión de manera temprana, como reitero en el texto principal, al final del día se centran en la aplicación de fuerza bruta computacional. La victoria de DeepBlue sobre Kasparov en 1997, mientras que prueba significativa del avance en la velocidad de procesamiento, no era un cambio cualitativa en la capacidad de los ordenadores de descubrir estrategias de comportamiento óptimo. De igual manera que un ordenador puede calcular muchísimo más rápido que cualquier humano, un ordenador moderno puede evaluar muchos más movimientos de ajedrez, pero en cierto sentido no hay “mayor secreto” en ello.
{ 19 comentarios… léelos a continuación añade uno }
https://www.shadertoy.com/view/MdV3Wh
https://www.shadertoy.com/view/4dVGWw
Murphy http://people.ischool.berkeley.edu/~hal/Papers/2013/ml.pdf
AlphaGo es un gran logro de la ingeniería. Las ideas básicas estaban ahí hace tiempo (1) (la última, hace diez años) pero el aumento en la potencia de cálculo y el esfuerzo de unas mentes brillantes consiguió este espectacular resultado. Aún así, pienso que aún queda un largo camino hasta llegar a Terminator:-)
(1) La primera idea es el “aprendizaje por refuerzo”que enlaza con algo -creo- familiar a los economistas, la programación dinámica. Samuel aplicó con éxito esta idea a finales de los 50:
https://webdocs.cs.ualberta.ca/~sutton/book/ebook/node109.html
https://www.cs.virginia.edu/~evans/greatworks/samuel1959.pdf
y Tesauro logró un gran éxito en los 90 al aplicarla al backgammon:
http://www.bkgm.com/articles/tesauro/tdl.html
https://webdocs.cs.ualberta.ca/~sutton/book/ebook/node109.html
https://www.cs.virginia.edu/~evans/greatworks/samuel1959.pdf
y Tesauro logró un gran éxito en los 90 al aplicarla al backgammon:
http://www.bkgm.com/articles/tesauro/tdl.html
(2) La 2ª idea es la del “deep learning”:
http://www.cs.toronto.edu/~hinton/absps/NatureDeepReview.pdf
Tesauro empleó una red neuronal sencilla para conseguir un programa que jugaba al backgammon mejor que cualquier humano; pero para dominios más complejos es necesario emplear redes más sofisticadas. Hace un año Google presento DeepMind, un sistema que emplea redes neuronales “deep” que alcanzó prestaciones expertas en los “arcade games”:
https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf
https://www.youtube.com/watch?v=V1eYniJ0Rnk
Pero no hay que dejarse llevar por la palabrería: las redes neuronales son dispositivos que estiman funciones no lineales; ni más, ni menos.
http://www.cs.toronto.edu/~hinton/absps/NatureDeepReview.pdf
Tesauro empleó una red neuronal sencilla para conseguir un programa que jugaba al backgammon mejor que cualquier humano; pero para dominios más complejos es necesario emplear redes más sofisticadas. Hace un año Google presento DeepMind, un sistema que emplea redes neuronales “deep” que alcanzó prestaciones expertas en los “arcade games”:
https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf
https://www.youtube.com/watch?v=V1eYniJ0Rnk
Pero no hay que dejarse llevar por la palabrería: las redes neuronales son dispositivos que estiman funciones no lineales; ni más, ni menos.
(3) La 3ª idea, específica de los juegos bipersonales, es MonteCarlo Tree Search:
https://en.wikipedia.org/wiki/Monte_Carlo_tree_search
Desde 2006 (el año de la revolución deMonte Carlo en juegos) la técnica empezó a ser explotada sistemáticamente en los programas de Go.
https://en.wikipedia.org/wiki/Monte_Carlo_tree_search
Desde 2006 (el año de la revolución deMonte Carlo en juegos) la técnica empezó a ser explotada sistemáticamente en los programas de Go.
Google liberó el código de uno de sus algoritmos de redes neuronales, el TensorFlow. El mundo va muy deprisa.
https://www.quora.com/How-will-machine-learning-impact-economics?redirected_qid=6706789
Susan Athey, Stanford University and NBER and Guido Imbens, Stanford University and NBER Organizers
https://vimeo.com/136531605
-Guido Imbens
Introduction to Supervised ML Concepts and Algorithms
http://www.nber.org/econometrics_minicourse_2015/
Fuente articulo:
http://nadaesgratis.es/fernandez-villaverde/aprendizaje-profundo-i
Susan Athey, Stanford University and NBER and Guido Imbens, Stanford University and NBER Organizers
-Susan Athey
Machine Learning and Causal Inference
https://www.gsb.stanford.edu/faculty-research/faculty/susan-atheyMachine Learning and Causal Inference
https://vimeo.com/136531605
-Guido Imbens
Introduction to Supervised ML Concepts and Algorithms
http://www.nber.org/econometrics_minicourse_2015/
Fuente articulo:
http://nadaesgratis.es/fernandez-villaverde/aprendizaje-profundo-i
http://nadaesgratis.es/fernandez-villaverde/aprendizaje-profundo-ii
Aprendizaje profundo II
La semana pasada describí algunas de las ideas fundamentales detrás del aprendizaje automático. Hoy me toca, como prometí, presentar un brevísimo repaso de las ideas de aprendizaje profundo y su uso de redes neuronales artificiales de múltiples capas.
Neuronas Artificiales
Para ello mi primer cometido es explicar que es una neurona artificial. En la mayoría de los libros de texto, y como uno sospecharía por su propio nombre, las neuronas artificiales y el vocabulario de las mismas se motivan por su analogía con las neuronas naturales existentes en el sistema nervioso de los seres humanos.[1] Y aunque no quiero quitar mérito alguno a tal analogía, que estoy seguro funciona fenomenal con estudiantes provenientes de ingeniería o de ciencias naturales (o dejar de citar a nuestro grandísimo Ramón y Cajal), mi experiencia es que para los estudiantes de economía, quizás como consecuencia de sus menores conocimientos de biología, tal motivación confunde más que ayuda.
Mi explicación habitual cuando enseño a estudiantes de grado en economía enfatiza las neuronas artificiales son una forma de regresión no lineal muy similares a los logits (una idea con la que los economistas ya están familiarizados) y limita, en la medida posible, el uso de vocabulario que sea diferente del que empleamos habitualmente en econometría. Como tales regresiones no lineales, una neurona artificial no es más que una aproximación flexible a una esperanza condicional desconocida.
Más en concreto, una red neuronal es una transformación no lineal de una combinación lineal de variables. Primero, tomamos
variables observadas
dados unos pesos . La primera variable puede ser una constante y por tanto su peso se llama a veces el sesgo (o intersección en la terminología de regresiones). Segundo, transformamos con una función no-lineal:
Volviendo a mi explicación como esperanza condicional. Un agente se encuentra con el problema de decidir cuál es la esperanza de una variable condicional en unas variables observadas o, más concretamente, (que esta relación sea causal o no es irrelevante en este momento; solo estamos buscando un predictor).[2] Sin embargo, esta esperanza condicional es desconocida y la aproximamos como:
Esta estrategia funcionará de manera más que satisfactoria en circunstancias normales porque sabemos una función desconocida con ciertas propiedades de regularidad puede ser aproximada arbitrariamente bien con estas regresiones no lineales.
Un ejemplo muy sencillo clarifica la notación y la explicación de la esperanza condicional. Imaginemonos que somos una cadena de supermercados y queremos predecir el número de botellas de mi leche favorita que vamos a vender esta semana en nuestras distintas localizaciones en el area metropolitana de Filadelfia. Podemos seleccionar como variables características demográficas del vecindario (número de habitantes, edad media, renta media, etc.), temporales (temperatura esperada), ventas pasadas, etc. Cada una de estas variables es asignada un peso (volveremos en unos párrafos a cómo tales pesos se determinan, por el momento imaginémonos que un consultor profesional nos los da) y obtenemos un valor . La función transforma ese valor en una predicción de ventas para cada localización.
Llegados a este punto, mis lectores con ciertos conocimientos de economía se estarán preguntado cuál es la novedad de este enfoque con respecto a las regresiones no lineales que llevamos estimando desde hace al menos 60 años. La respuesta es que ninguna. La separación de la no linealidad en mientras mantenemos la estructura lineal en es conveniente, pero no deja de ser un detalle. Lo interesante viene ahora.
Redes Neuronales
Las neuronas artificiales se pueden combinar en diferentes capas para crear redes neuronales. Volviendo a nuestra notación anterior. Nuestras variables se organizan en una primera capa con distintas combinaciones lineales de los mismas:
cada una de ellas con pesos . Notemos que ahora los pesos están indiciados tanto por la combinación lineal, en los subíndices , como por la capa, en el superíndice.
Regresando a nuestro ejemplo de predicción de las ventas de botellas de leche en una cadena de supermercados: en vez de construir una sola variable , lo que hemos hecho ahora es construir diferente 's, cada una de las mismas con unos pesos distintos. La variable puede, imaginémonos, tener pesos más grandes en las variables demográficas y la variable puede preferir, en comparación, ponderar más las variables como ventas pasadas.
Las variables se pueden combinar, a su vez, en una función o emplear como insumos en una segunda capa:
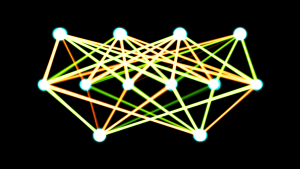
cada una de ellas con pesos . Estas segundas variables son las que se pueden combinar a su vez en una función o servir como insumos en una tercera capa. Es más podemos emplear todas las capas que consideremos necesarias (los libros de texto mencionan que en el cerebro humano las neuronas se organizan hasta en seis capas; carezco de conocimientos para juzgar la exactitud de esta afirmación). Estas capas intermedias se suelen llamar capas ocultas, la capa inicial se suele llamar capa de entrada y la agregación con la función , capa de salida. El gráfico que inaugura esta entra es una representación de una red neuronal artificial con una capa de entrada y dos capas ocultas.
Aquí es importante señalar dos puntos. Primero, que el número de variables en la segunda capa puede ser igual o distinto del número de variables en la primera capa (o en cualquier otra capa). De igual manera podemos cambiar la función en cada capa. Ambas son decisiones del investigador (o quizás del algoritmo, si le damos flexibilidad para ello). Segundo, que esta estructura de capas no es mágica: no hay información nueva alguna diferente de las variables observadas . Lo único que hacemos con las distintas capas es crear una ponderación de las mismas altamente no lineal, lo que permite aproximar esperanzas condicionales particularmente complejas, pero en módulos lineales, lo cual es util para su implementación numérica práctica. De hecho, me estoy saltando todos los resultados matemáticos que demuestran relaciones de equivalencia entre distintas estructuras de una red y su posible reducción a una capa única.
Finalmente, y solo por enlazar con las partidas de go que sirvieron como motivación a esta serie, una red neuronal puede ser empleada para evaluar la situación de las fichas en el tablero en un momento determinado de la partida. En el caso del ajedrez, el ordenador sabe donde está cada caballo, torre o peón y, dados unos pesos, encuentra un valor asociado a esta situación. Una vez que tenemos la red neuronal, solo necesitamos que el ordenador encuentre todos los posibles movimientos a partir de la situación actual, compute todas las posibles respuestas del rival (iterando por varios movimientos y eliminando algunas ramas del árbol de movimientos que claramente están dominadas), evaluar el valor asociado a casa situación final después de esos movimientos y seleccionar el movimiento que maximiza tal valor (quizás jugando algún tipo de maxmin). En el caso de go, esta misma estrategia sufre de cuatro problemas. Primero, el tablero es más grande, con lo cual es más complejo capturar su situación con una red neuronal. Segundo, existen muchos más movimientos legales en cada momento (unos 250 en go frente a unos 35 en ajedrez), con lo cual es más difícil computar el valor al final de varias iteraciones. Tercero, al ser todas las fichas iguales (en ajedrez una reina es más valiosa que una torre y tenemos valores convencionales del valor relativo de las fichas que funcionan bien casi siempre), es más intrincado definir unos pesos en la red neuronal que encuentre valores en las posiciones futuras. Cuarto, las partidas suelen durar más (unos 150 movimientos en go frente a unos 80 en ajedrez). Estos cuatro problemas son lo que también empujan a los jugadores humanos de go a emplear la intuición y la imitación de los grandes maestros del pasado más que en ajedrez.
Encontrando pesos
En las dos secciones anteriores he descrito qué es una neurona artificial, cómo se pueden agrupar distintas neuronas en redes neuronales y cómo con estas redes podemos predecir o asignar un valor a una situación en el tablero (o recomendarnos que película queremos ver en Netflix). En toda la discusión, sin embargo, siempre asumí que conocíamos los pesos de la red y que sabíamos qué función emplear.
Ahora me voy a centrar, por tanto, en cómo encontrar estos pesos (las familias de funciones a emplear es más sencilla de explorar, con candidatos naturales como logits). La estrategia más sencilla es estimarlos con datos observados. Obtenemos muchas y muchas y buscamos los pesos que minimizan la distancia (según algún tipo de métrica) entre las observadas y las generadas por la red neuronal. Este problema de minimización es normalmente complejo y es preciso emplear técnicas relativamente sofisticadas, como elgradiente de descenso estocástico, para evitar quedarse atrapado en mínimos locales y encontrar los mínimos globales.[3] De igual manera, y cuando se tienen diferentes capas, hay que ser cuidadoso en como se ajustan los pesos en cada capa (con una propagación hacia atrás; a riesgo de simplificar quizás en exceso y pidiendo disculpas por ello: encontrando derivadas de los errores con respecto a los pesos empleando la regla de la cadena).
Una estrategia que a menudo funciona muy bien, y que yo he empleado en otros contextos, pertenece la familia de algoritmos genéticos:
1) Comenzamos con, por ejemplo, 10.000 valores iniciales de los pesos diferentes generados aleatoriamente. Cada uno de estos 10.000 valores iniciales definen una red neuronal particular.
2) Calculamos entonces cómo de bien cada una de las redes predice los datos. Este paso, en evolución, es la medida de aptitud de una estructura genética a su medio.
3) Seleccionamos, con reemplazo, 10.000 redes neuronales de entre las 10.000 que tenemos según su medida de aptitud. Es decir, las redes que han ajustado los datos mejor tienen una probabilidad más alta de ser seleccionadas y las redes que han ajustado peor una probabilidad más baja. La clave es que esta selección es con reemplazo: la red neuronal 2.345, que ajusta muy bien, puede ser seleccionada cuatro veces mientras que la red neuronal 4.531, que ajusta mal, es seleccionada en cero ocasiones. Como en evolución, las configuraciones genéticas con mayor aptitud tienen una probabilidad más alta de supervivencia y reproducción.
4) Y de igual modo que en la reproducción, ocurrirán mutaciones. Los pesos de la red neuronal 2.345 seleccionada para sobrevivir en el segundo paso del algoritmo no serán los mismos que los de la red 2.345 en la iteración anterior. Introduciremos un pequeño movimiento aleatorio en los mismos. Por ejemplo, si de la red 2.345 en la iteración 1 es 56.98, en la iteración 2 sera 56.98+innovación, donde innovación viene de una distribución Gaussiana (u otra distribución conveniente) con la escala adecuada (hay que encontrar un balance entre mutaciones novedosas y movimiento excesivo de las mismas).
5) Repetimos los pasos 2)-5) varios miles de veces.
6) Al final de la última iteración nos quedamos con la red neuronal que, a lo largo de toda la iteración, se haya ajustado mejor a los datos.
Es importante notar que el algoritmo recoge las dos ideas claves de la evolución: supervivencia (estocástica) de los más adaptados y mutaciones (también estocásticas) que generan nuevas estructuras genéticas. Las mutaciones son las que nos evitan quedarnos en mínimos locales y, bajo ciertas condiciones topológicas de la cadena de Markov implicada por el algoritmo descrito como la recurrencia de Harris en las que no quiero entrar, convergeremos al mínimo global con probabilidad 1. De igual manera, si el lector sabe algo de programación, se habra dado cuenta que este algoritmo son menos de 100 lineas en Julia: es facilísimo de programar y de correr.
En el caso de la predicción de la venta de leche, es obvio como implementar este algoritmo genético. En el caso de las redes neuronales en ajedrez o go, se puede modificar para que las redes jueguen con partidas históricas (en un primer paso), entre ellas (en un segundo paso) o contra seres humanos (en un tercer paso) y en vez de seleccionar las redes que ganan las partidas más a menudo. Esta fue la estrategia de AlphaGo.
Aprendizaje profundo
Finalmente, después de bastante trabajo preliminar, estamos en una situación en la que puedo explicar qué son las técnicas de aprendizaje profundo. Las redes neuronales tradicionales (u otros mecanismos semejantes) tienen un alto grado de estructuración: el diseñador de las mismas decide, basándose en su conocimiento del problema, el número de capas, neuronas, variables observadas, etc. En el ejemplo de la predicción de ventas de leche, el economista tiene que decidir qué variables son relevantes, ponerlas en un formato adecuado (como un fichero con los datos limpios y fáciles de leer por el ordenador), introducirlas en la código, etc. Las técnicas de aprendizaje automático más comunes pueden ayudar en seleccionar las pesos (como describimos antes) o incluso las variables posibles (con un búsqueda voraz como la expuesta la semana pasada), pero al final del día, el ordenador solo puede moverse dentro de un contexto muy estructurado.
Las técnicas de aprendizaje profundo buscan diseñar algoritmos en los cuales podamos dar al ordenador los datos en bruto (por ejemplo, muchos datos demográficos y de venta de leche) y que el ordenador mismo descubra cuáles son los datos relevantes y la estructuración de los mismos, reduciendo así al mínimo los insumos por parte del diseñador humano y facilitando la aplicación del algoritmo a situaciones nuevas y diferentes.
En particular, los algoritmos de aprendizaje profundo emplean cada una de las muchas capas de una red neuronal (o técnicas semejantes) para representar un nivel de abstracción diferente. Una estructura particularmente exitosa de estructurar estas capas múltiples han sido las redes neuronales convolucionales que propusieron Yann LeCun y sus coautores. Estos días las arquitecturas de las redes neuronales convolucionales tienen hasta 20 capas de unidades rectificadoras lineales. Además, estas múltiples capas pueden ser entrenadas con los algoritmos descritos en la sección anterior gracias a la generalización de las GPUs, que permiten la computación masiva en paralelo a un coste muy razonable (aquí un trabajo mío sobre el tema; AlphaGo emplea 280 de estas GPUs).
En el caso de AlphaGo, el programa tiene dos clases diferentes de redes neuronales con múltiples capas. Unas redes, llamadas redes de valor, evalúan la situación en el tablero. Unas segundas redes, llamadas redes de política, evalúan movimientos. Esta división en dos módulos diferentes es particularmente inteligente: en vez de buscar entre todas los posibles movimientos (como se hace en ajedrez, una vez eliminados los movimientos claramente inferiores), la red de política proponen un conjunto razonablemente reducido de movimientos que la red de valor evalúa. La posición el tablero es pasada a unas capas convolucionales como las que mencionábamos anteriormente. Los pesos fueron ajustados, primero mirando a movimientos de seres humanos expertos y posteriormente con ligeramente distintas versiones de las redes jugando entre ellas. Esta estrategia soluciona el problema de cómo evaluar la posición en el tablero de una manera muy diferente que en los programas de ajedrez: estos, por las razones expuestas anteriormente, podían emplear los conocimientos de expertos humanos para definir los pesos necesarios (quizás con ciertas mejoras por simulación). Pero en go no se podía hacer: incluso los mejores expertos tenían problemas en verbalizar porque unas situaciones del tablero eran mejores que otras. Es además el sentido en el que podemos decir que AlphaGo se ha enseñado a si mismo: los pesos no se los ha dado un ser humano, son producto de la evolución del sistema.
Concluyo aquí, ya acercándome a 3.000 palabras y con ello abusando de la paciencia incluso del lector más paciente, mi descripción de las ideas básicas del aprendizaje profundo. Los lectores con más conocimientos sobre estos temas sabrán que me he dejado más cosas en el tintero que las que he podido explicar y que, en varias ocasiones, he simplificado la explicación hasta peligrosamente acercarme a la incorrección. Por ejemplo, no he tenido tiempo de hablar de las redes neuronales recurrentes, que tanto interés han despertado en los tres últimos años. A fin de cuentas el material, para ser desarrollado en detalle, requeriría un libro de texto entero bastante largo (como este en preparación). Pero espero que los lectores con menos conocimientos hayan disfrutado, al menos, de una breve panorámica de las técnicas y las promesas de este campo y que los enlaces les sirvan para profundizar más lejos de mis brevísimas palabras.
2. Si en vez de la esperanza, buscamos otro momento como un percentil, solo tenemos que definir una función de interés de y
. Por ello limitarnos a la esperanza condicional no es restrictivo. Si tuviese más espacio, explicaría como podemos movernos de predictores a investigar causalidad. Es suficiente para mi propósito señalar que no hay nada especial en el tratamiento de causalidad en este campo y que aprendemos con las técnicas habituales (como variables instrumentales o experimentos) sigue funcionando aquí con sus fortalezas y debilidades.
3. Sorprendentemente en muchas ocasiones los investigadores han descubierto que distintos mínimos locales producen ajustes que son prácticamente indistinguibles en término de predicción.
Tapping the supercomputer under your desk: Solving dynamic equilibrium models with graphics processors$ Eric M. Aldrich a,f,, Jesu´ s Ferna´ndez-Villaverde b,c,d,e , A. Ronald Gallantf,g , Juan F. Rubio-Ramı´rez a,e
This paper shows how to build algorithms that use graphics processing units (GPUs) installed in most modern computers to solve dynamic equilibrium models in economics. In particular, we rely on the compute unified device architecture (CUDA) of NVIDIA GPUs. We illustrate the power of the approach by solving a simple real business cycle model with value function iteration. We document improvements in speed of around 200 times and suggest that even further gains are likely. & 2010 Elsevier B.V. All rights reserved.
http://economics.sas.upenn.edu/~jesusfv/GPU_Computing.pdf