Ni el pico ni el final de una epidemia se pueden predecir con precisión
Vuelvo antes de lo previsto a Nada es Gratis para comentar un artículo aparecido en el servidor de preprints arXiv el martes 21 de abril, y titulado “Predictability: Can the turning point and end of an expanding epidemic be precisely forecast?” (“Predecibilidad: Pueden predecirse con precisión el pico y el final de una epidemia en expansión?”).. Como desde el principio de la pandemia he estado muy preocupado por el elevadísimo número de trabajos basados en modelos más o menos realistas que produce la comunidad de físicos y matemáticos (cuando escribo esto hay 506 preprints en arXiv con la palabra “covid” en el título), el título me llamó la atención, y entonces me fui al abstract y ví que la respuesta era “No, no se puede”, en línea con mis sospechas. Así que me fui al artículo y, en mi opinión, lo que encuentran los autores (Mario Castro, Saúl Ares, José A. Cuesta y Susanna Manrubia, que aclaro que además de buenos científicos son amigos, e incluso han contribuído a este blog, aquí y aquí) es muy importante para poner la discusión sobre predicciones en contexto (y para justificar mi vuelta repentina). Básicamente, amigo lector, el mensaje es que predecir estas epidemias es como predecir el tiempo, y más allá de dos o tres días el error es enorme, con lo que hay que tomarse todas las predicciones con muchísima precaución; de hecho, lo mejor es pasarse a la predicción probabilística. Resumido pues el mensaje del trabajo para el lector con poco tiempo, vayamos a algo más de detalle.
El concepto fundamental que hay detrás del resultado del artículo es el de “caos“. En un post de hace ya casi siete años, ya hablé en detalle del trabajo de Edward Lorenz y su descubrimiento del caos, consagrado en una charla legendaria titulada «Predictibilidad: ¿El aleteo de las alas de una mariposa en Brasil provoca un tornado en Texas?»,
de la que imagino que los autores toman el título de su trabajo. Al
introducir ese concepto, Lorenz había descubierto también una de sus
mayores consecuencias: la impredecibilidad del tiempo (meteorológico).
Por medio de un simple modelo, demostró que nunca se puede estar seguro
de si, de aquí a una semana, tendremos un día soleado o uno
lluvioso. Medio siglo después, estamos acostumbrados a escuchar el
pronóstico del tiempo en términos de porcentajes, probabilidad de
lluvia, intervalos de temperatura o velocidad del viento. «El tiempo»
ocupa una buena parte de los informativos y es todo un alarde de
tecnología e información. En ocasiones, es un tanto confusa, pero
normalmente suficiente para decidir qué hacer el próximo fin de semana,
aunque aceptamos con normalidad que hay incertidumbre en la predicción y
que nuestros planes pueden truncarse a última hora.
Matemáticamente, esta incapacidad para predecir más allá de unos
pocos días se debe a la amplificación exponencial de pequeñas
diferencias iniciales prototípicas de los sistemas caóticos. Pero como
mi sufrido lector ya habrá oído en las últimas semanas, todos los
esfuerzos sociales y económicos a los que estamos haciendo frente tienen
como objetivo «aplanar la curva»… exponencial. La exponencial
es una función bien conocida y a la que nos aproximamos por primera vez
en la educación secundaria a través de la progresión geométrica
(Matemáticas) o el interés compuesto (Economía). Veamos ahora cómo
conecta esto con las predicciones epidemiológicas.
Como ya he dicho, dado el impacto de la pandemia de COVID-19, gran
número de epidemiólogos, estadísticos, matemáticos, físicos o
economistas se han lanzado al modelado y predicción de la epidemia (di ejemplos en este post reciente, y aquí
hay alguno más del que se ha hablado en NeG). La mayoría utilizan
modelos tradicionales de la epidemiología, en los que se divide la
población en categorías (o «compartimentos»): susceptibles (S),
infectados asintomáticos (E), infectados sintomáticos (I), recuperados
(R), fallecidos (D) y varias otras posibles etapas intermedias como en
cuarentena, hospitalizados o en la unidad de cuidados intensivos (UCI).
Las iniciales de las categorías principales dan nombre a los modelos
(SIR, SEIR, etc., aunque a esta sopa de letras de denominaciones se la conoce genéricamente como «SIR»).
Más allá de su clara interpretación y facilidad de uso, una de las
principales motivaciones para aplicar esos modelos es tratar de estimar
las próximas etapas de la epidemia y cuantificar los efectos de las
medidas no farmacéuticas para «aplanar la curva». Un objetivo práctico
(tal vez el más importante) es lograr controlar el número de camas en
UCIs necesarias cuando la enfermedad alcanza su punto máximo en cada
país o región, y eso, claro está, requiere predicciones cuantitativas y
precisas.
En este contexto, los autores del trabajo se preguntan hasta qué
punto somos capaces de predecir cuándo llegará la expansión de la
epidemia a su máximo, cuál será el número final de fallecidos o incluso
si el confinamiento tendrá el efecto deseado o no. Para responder,
plantean un modelo con los ingredientes esenciales de la epidemia
(infección/confinamiento/evolución de la enfermedad), pero que es lo
suficientemente sencillo como para analizarlo y poder ilustrar las ideas
principales de su argumento. En la figura, tomada de su artículo,
aparecen las distintas categorías en las que dividen la población y cómo
evoluciona de una categoría a otra.

Para poder alimentar el modelo, recurren a los datos oficiales
publicados por el Ministerio de Sanidad con reportes diarios de casos
confirmados, pacientes recuperados y fallecidos. A estas alturas de la
película, todos somos conscientes de las limitaciones de estos datos,
pero eso refuerza aún más el argumento acerca de la incertidumbre y la
predecibilidad. Como los autores también tienen esta preocupación,
intentan incorporar de manera probabilística esta ignorancia sobre los
parámetros, mediante un modelo Bayesiano.
Gracias a la simplicidad del modelo, se puede obtener una fórmula
aproximada para el valor efectivo del ritmo (o factor) reproductivo
básico, R0, una variable dinámica que cambia conforme las medidas de confinamiento van haciendo efecto:
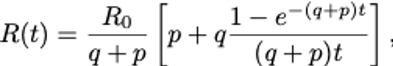
donde t es el tiempo, R0 es el valor al principio de la epidemia, antes de que se tome ninguna medida de control, q es tanto mayor cuanto más restrictivas sean las medidas de movilidad y distancia social, y p
cuantifica la falta de adherencia al confinamiento, ya sea por personal
sanitario o de servicios básicos que tienen necesariamente que salir de
casa, o simple y llanamente por tramposos que se saltan las reglas a la
torera. En el límite de tiempos grandes, el número
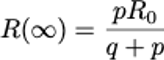
indica si el efecto del confinamiento será suficiente para alcanzar
un pico y doblegar la curva: ocurrirá cuando este número sea menor que
1.
Una de las cosas interesantes que se aprenden del modelo es que
«aplanar la curva» no es, ni mucho menos, sinónimo de controlar la
epidemia. El confinamiento siempre curva lo que, sin él, sería un simple
crecimiento exponencial. Esta curvatura se lleva interpretando desde su
aparición en los datos como un signo de que el control de la epidemia
se acerca. Lo que el modelo dice es que si R(∞) > 1, es decir, si las
medidas de confinamiento son insuficientes, la curva no se doblegará
hasta que, en promedio 1-1/R0 de la población se haya infectado (observe, amigo lector, que si R0 es
muy grande, casi toda la población se infectará). En tal caso, la
epidemia entraría en una segunda fase en la que simplemente crece como
una exponencial más lenta. Por contra, si R(∞) < 1 la epidemia
alcanza un máximo y luego empezará a decrecer el número de infectados.
En ambos casos se observa esa curvatura de la exponencial, de manera que
del hecho de aplanar la curva no aprendemos absolutamente nada. De
hecho, el carácter probabilístico del método Bayesiano hace que los
datos sean compatibles con distintos escenarios futuros, en algunos de
los cuales se controla la epidemia y en otros no.
Conclusión: en la parte creciente de la curva, cuando la epidemia
está aún expandiéndose, lo más que podemos afirmar es que los datos
indican que la epidemia se controlará con una determinada probabilidad.
En el caso de los datos que se proporciona diariamente para España el
Ministerio de Sanidad, tomando la serie hasta el 29 de marzo (partiendo
de que el confinamiento empezó con los colegios el 11 de marzo), lo
único que se podía afirmar es que el pico se alcanzaría con una
probabilidad de una entre cuatro. Esto es lo que recoge la siguiente
figura (casos activos en vertical, en función de los días desde el
primer caso confirmado):
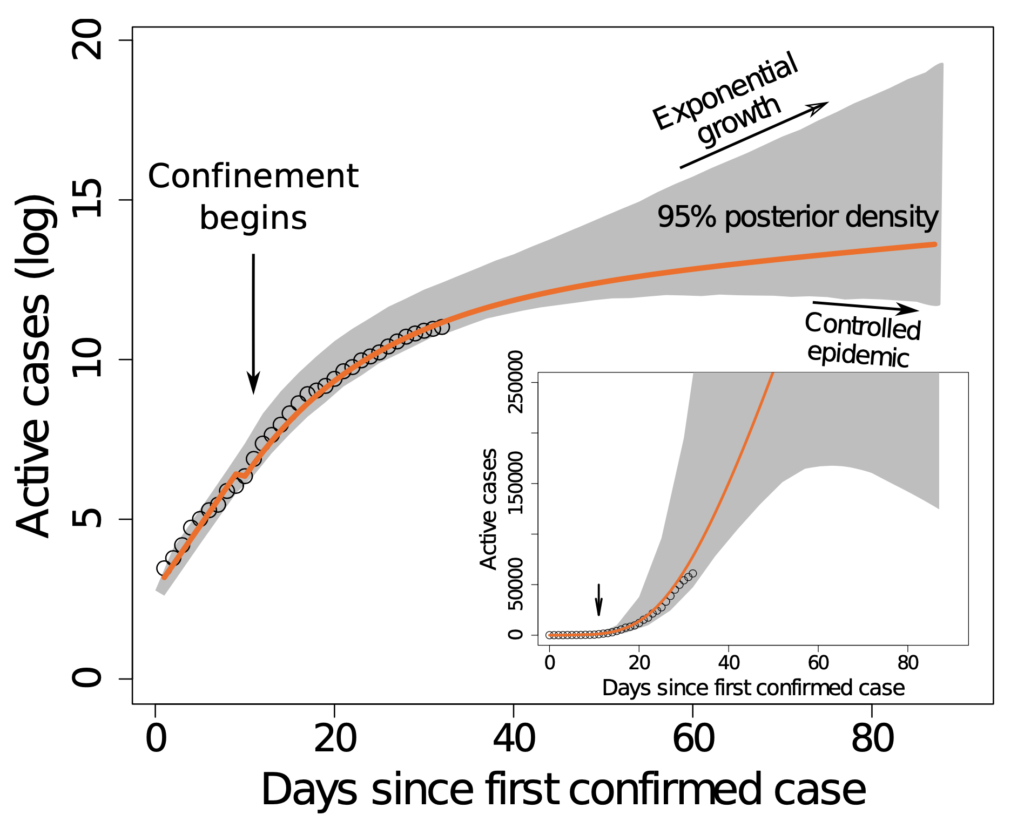
En esta figura se muestra la misma información de dos maneras, por un
lado, en escala logarítmica, donde sólo nos importan los órdenes de
magnitud de la epidemia y, por otro, en el recuadro interior, la misma
información en escala lineal. En la escala logarítmica se ve que las
medidas de contención pueden dar lugar a una segunda fase exponencial o
bien a una epidemia controlada. En la escala lineal (en la que
lamentablemente se sigue presentando la información en muchos medios, o
incluso se validan algunos modelos matemáticos) se ve que el grado de
incertidumbre sobre el final del proceso es dramático (zona sombreada).
Aquí es dónde mi avispado lector se da cuenta de que esta conclusión
suscita más preguntas que respuestas, y se plantea si la incertidumbre
se debe al modelo que han elegido los autores (elegido con cuidado para
que salga el resultado), a la mala calidad de los datos, o es en
realidad algo intrínseco de la dinámica de las epidemias. No se
preocupe; los autores del estudio también se lo han planteado, y lo que
ven es que este fenómeno es algo intrínseco a la dinámica de la
epidemia. Para ilustrarlo, toman los parámetros que resultan del ajuste
anterior (la curva naranja de la figura) y generan los datos a ajustar
con el propio modelo determinista. Es decir, con su propio modelo
producen unos números y, lógicamente, los ajustes del mismo modelo
deberían describirlos perfectamente. O dicho de otro modo, la calidad de
los datos que se utilizan ahora es perfecta. Sobre esos datos, hacen la
misma inferencia bayesiana que con los datos originales, y resulta la siguiente figura (mismos ejes que antes):
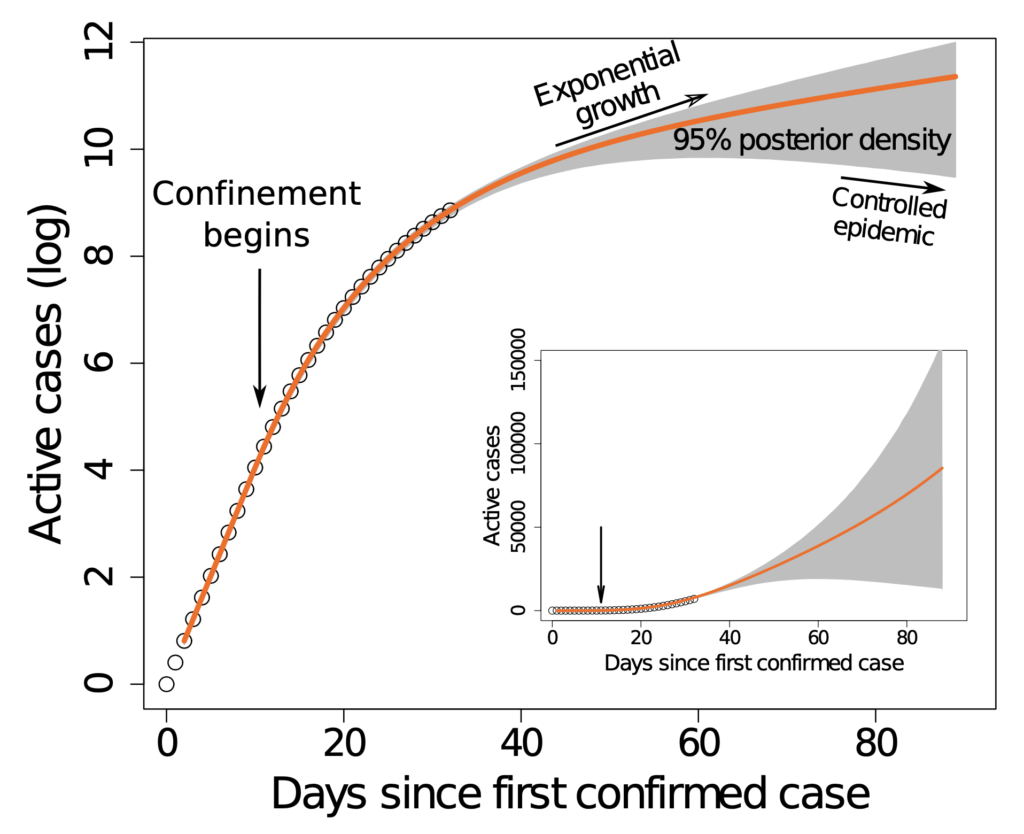
Como se puede ver, la incertidumbre es nula mientras estamos en los
datos suministrados, pero en cuanto tratamos de hacer una predicción a
futuro, la incertidumbre se abre en abanico y, de nuevo, es compatible
con escenarios muy distintos. Esto demuestra que la imprecisión de los
datos, que sólo puede complicar las cosas, no es la razón profunda de
esta incapacidad para predecir.
Lógicamente, nos queda la otra pregunta, la relativa a si la
conclusión aparece por la simplicidad del modelo. Lógicamente también,
responderla requeriría hacer un estudio exhaustivo de distintos modelos
(que ya hemos visto que son centenares). Sin embargo, los autores dan un
argumento que sugiere que todos se van a encontrar el mismo problema.
Recordemos que cualquier modelo epidemiológico tiene que explicar, en
primer lugar, el crecimiento exponencial en la fase inicial de la
pandemia. Una exponencial es extremadamente sensible a la incertidumbre
en los parámetros, de manera que pequeñas variaciones en estos pueden
dar lugar a predicciones divergentes igual que le ocurría al bueno de
Lorenz. Añadir nuevas categorías para asintomáticos, y estratificar los
datos por edades, movilidad geográfica, antecedentes médicos, nivel
socioeconómico, etc., desde luego aumenta la fiabilidad de las
predicciones a corto plazo, pero la amplificación exponencial dará al
traste con la de las predicciones a largo plazo. Lo que resulta
preocupante de emplear modelos sofisticados es que pueden crear una
falsa percepción de realismo y minuciosidad que nos impide percibir que
adolecen del mismo problema a largo plazo. Si se da cuenta, los modelos
meteorológicos son extraordinariamente detallados y sofisticados, y ni
por esas predicen bien una semana.
Enonces, ¿qué concluimos de este trabajo? ¿Que está todo perdido? ¿Es
este un mensaje pesimista y negativo, y mejor vamos a darnos a la
bebida para olvidar (no, que los bares están cerrados y beber solo en
casa no es bueno)? Pues la verdad es que no, y en realidad la predicción
meteorológica nos marca el camino a seguir. Para empezar, debemos
abandonar la predicción determinista y asumir la incertidumbre inherente
a estos procesos aceptando predicciones probabilísticas. Ya hay grupos
consolidados en todo el mundo que han adoptado este enfoque (como el de Imperial College,
que sin duda empujó al gobierno de Boris Johnson a cambiar su
estrategia) y que permiten generar múltiples escenarios y no sólo uno
como si la trayectoria futura de la epidemia se pudiese predecir
sencillamente con los datos pasados y estuviese «ahí», esperando a ser
descubierta. Por otra parte, necesitamos mejores medidas (el equivalente
a los globos y las estaciones meteorológicas), con una granularidad
suficientemente amplia. Y finalmente, necesitamos un plan global (a
escala planetaria) para adoptar un enfoque unificado, donde la
información sea compartida y detallada y donde los modelos, sus
supuestos y sus conclusiones sean transparentes y realistas.
Aprendamos del pasado y confiemos en que el coronavirus nos deje, al menos, este legado positivo.
Nota importante: como en este blog he hablado muchas
veces de predicciones sobre cambio climático, me veo obligado a aclarar
que no es lo mismo predecir el tiempo que va a hacer dentro de dos o
tres días que el clima que va a hacer dentro de uno o varios años
(spoiler: por estas fechas el año que viene será primavera). No quiero
que esta confusión, que hizo famosa Rajoy,
se malinterprete y se aplique a que el clima no se puede predecir. Y
dicho eso, las predicciones del IPCC son siempre probabilísticas, y
asignan high confidence (“alta confianza”) cuando la
probabilidad de que algo pase es mayor que el 90%. Y sí, que si no
hacemos nada antes de 2050 habremos aumentado la temperatura media del
planeta en dos grados respecto a niveles preindustriales tiene “mucha high confidence“.
Anxo Sánchez
Anxo Sánchez es Doctor en Física Teórica y Matemática por la Universidad Complutense de Madrid y Catedrático de Matemática Aplicada en la Universidad Carlos III. Tras dedicar quince años a estudiar solitones, dispositivos semiconductores y crecimiento de materiales, en los últimos años sus áreas de investigación tienen que ver con las aplicaciones de herramientas físicas y matemáticas en campos que van desde la biología a la economía, casi siempre desde la perspectiva de los sistemas complejos.https://nadaesgratis.es/anxo-sanchez/ni-el-pico-ni-el-final-de-una-epidemia-se-pueden-predecir-con-precision?fbclid=IwAR398NPWVPmI7rw3DprI6-SezxstgqevA03dr88dnVrtYuzPgxTByihRCVw
No hay comentarios:
Publicar un comentario