Parte I
"... once we begin to uncover the real factors affecting the performance of the economic system, the complicated interrelations between them will clearly necessitate a mathematical treatment, as in the natural sciences"
Ronald Coase, 1992
En un principio era Adán
... Adán Smith... pero no, en realidad todo comenzó mucho antes cuando un mallorquín, Ramon Llull, empezó a estudiar los sistemas de votación adelantándose 500 años a Condorcet y Borda...
Como muchos saben, nuestro Adán forjó su sistema sobre un postulado, a saber, que la productividad depende de la división del trabajo, que por algo es la primera frase del capítulo 1. ¿Prueba? En la página siguiente dice "Yo he visto una pequeña manufactura..." y describe cómo ahí se dividía el trabajo [2]. Y para rematar "En cualquier otro arte o manufactura los efectos de la división del trabajo son similares al pequeño ejemplo anterior". Para continuar con afirmaciones sobre la productividad del campo en Inglaterra, Francia y Polonia que no contienen ni un solo dato. Como no lo hay en su libro III, una especie de interpretación económica de la historia avant la lettre en donde el libre comercio es el prota bueno de la peli mientras que las únicas cifras (sobre el tonelaje de una pesquería) se relegan a un apéndice del libro IV.
Motivado por la obra del anterior, David Ricardo, descansando de sus rentables andanzas como especulador, mostró cómo dos países pueden comerciar ventajosamente incluso si uno de ellos es mejor que el otro en la producción de todas las mercancías. Y aquí viene su famoso ejemplo numérico en el que Portugal tiene ventaja absoluta sobre Inglaterra en la producción de paño y vino, pero el comercio aumenta la producción de ambos países [3]. Después de algún otro ejemplo, la materia se da por demostrada en general.
Carlos Marx se empeña en probar que la acumulación se produce principalmente en capital físico y no genera plusvalía. Para ello recurre a otro ejemplo numérico con el capital variable y el constante. Debe registrarse que Marx emplea muchos más ejemplos numéricos que sus antecesores y presenta bastantes estadísticas. Hay en su libro un intento serio de dotar de un elemento cuantitativo a sus razonamientos teóricos que, desgraciadamente, no se transmitió a sus seguidores.
Pasamos revista ahora a Staley Jevons que explica la paradoja del agua y los diamantes [4] que tantos dolores de cabeza produjo a los economistas clásicos. Usa un gráfico en el que comenta que "la utilidad de último incremento es pequeña". Se supone que esa intuición es general y que con ella podemos desentrañar el siempre lioso tema de la demanda de mercancías. A todo esto, gráficos y matemáticas relativamente avanzadas ya habían sido usados por dos genuinos representantes de la economía moderna empotrados en el siglo XIX, Cournot y Dupuit, que pusieron los fundamentos de las teorías del oligopolio y el análisis coste beneficio.
Otro de los fundadores de la economía neoclásica es Leon Walras que intenta unir todos los retazos en una tela consistente, el equilibrio general. Y usa muchos símbolos y ecuaciones. E inmediatamente surge la pregunta: ¿tendrán todas esas ecuaciones solución? Y razona "Las ecuaciones de materias primas y dinero constituyen un conjunto de 3m+2s+3 ecuaciones apto para determinar las 3m+2s+3 incógnitas" y así sucesivamente. En su descargo cabe señalar que el instrumento matemático para resolver este problema no existió hasta que en 1941 el padre de la que sería uno de los críticos literarios más influyentes del stage NY, Michiko Kakutani, generalizó el teorema del punto fijo de Brouwer (1910) [5].
En los años 20, gracias en buena parte a ese liante llamado Marshall, la profesión se enzarzó en la controversia de los rendimientos crecientes. Ya Cournot había resuelto el problema a saber, que costes marginales decrecientes y competencia perfecta eran incompatibles, lo cual venía a poner en solfa a las curvas de oferta decrecientes del británico a no ser que se postulasen economías de escala externas a la empresa e internas al mercado... pero tales economías se mostraron tan elusivas como el Tigre de Tasmania... Mientras tanto un genio llamado Frank Plumpton Ramsey había puesto las bases de las modernas teorías del crecimiento, la imposición y la interpretación subjetiva de la probabilidad. Murió a los 26 años. Por cierto, que, en 1927, el ingeniero Carlos de Orduña (padre del director cinematográfico) publicaba unas estimables Lecciones de Economía Matemática en las que, un año antes que los interfectos, presentaba una función de producción Cobb-Douglas ya propuesta por Walras y otros.
Y así llegamos a uno de los libros más famosos de economía del siglo XX La Teoría General escrito por otro habilidoso especulador que, a diferencia de muchos de sus antecesores, tenía educación matemática. Desgraciadamente a pesar de que ese libro contiene alguna ecuación y algún gráfico, el resultado es que, aún hoy, se siguen escribiendo artículos sobre lo que Keynes quiso decir realmente...
Después de la lluvia
... en la adecuada metáfora de Max Ernst, mucho capital humano europeo huyó al nuevo mundo. Aquellos con inquietudes de construir una gran ciencia social, se agruparon en Chicago y Princeton. Los primeros formaban parte de la Cowles Comission como Samuelson, Arrow, Koopmans y Hurwicz mientras que los segundos lo hacían alrededor de la universidad y el recientemente creado Institute for Advance Studies e incluían a uno de los grandes genios del siglo XX, John von Neumann así como una plétora de prometedores estudiantes como Nash, Shapley y Gale, hábilmente tutoreados por Tucker que unió su nombre a otro estudiante, Kuhn, en un paper que hizo fortuna en nuestra comunidad [6]. Los vimos en Una Mente Maravillosa.
Todas esas personas tenían un bagaje científico. Muchos eran matemáticos. Y al estudiar economía se dieron cuenta de que consistía en una colección de historietas, algunas muy fascinantes, pero que, en sí mismas, eran incapaces de fundamentar nada sólido. Y aquí señoras y señores empieza la economía de verdad. Con los teoremas de Arrow, Debreu y McKenzie, este último otro brillante estudiante de Princeton, aprendimos las condiciones bajo las cuales el sistema pergeñado por Walras tiene solución. Y cuándo el mercado es eficiente. Samuelson reescribió en forma matemática en un solo volumen todo lo que se había aprendido en teoría del consumo, producción, estabilidad y bienestar. Y mientras Arrow ofrecía su teorema de (im)posibilidad que aclaraba las controversias entre Condorcet y Borda, e inauguraba un nuevo campo, el de la Elección Social, Nash y Shapley ponían las bases de la teoría de juegos que estudia las situaciones de interdependencia, básicas para campos que fueron surgiendo como Organización Industrial, Diseño de Mecanismos, Teoría de las Contiendas, Economía Política, etc. Mincer, con su famosa ecuación, ponía las bases de la Economía del Trabajo y del Capital Humano, que tanto aprovecharon a Becker, North abría horizontes cuantitativos a la historia económica y apuntaba a las instituciones, de donde Acemoglu sacó petróleo y Solow escribía su modelo de crecimiento. Esto tenía que acabar como acabó, con estimaciones del PIB en tiempos de los romanos e incluso más allá, put the blame on Maddison, pero este enfoque nos ha dado una impresionante perspectiva sobre las andanzas de la humanidad que del neolítico a la revolución industrial hizo poca cosa...
La lista pergeñada en el párrafo previo, sería inacabable (añádanse la Economía de la Educación, de la Salud, Pública, Regional, Finanzas...). Todo lo que tiene que recordar el lector es que cuando le digan que la economía se dedica a estudiar mercados perfectos tiene que contestar "No sabes de lo que estás hablando". Y a los que dudan de la fecundidad del árbol matemático ponerles de ejemplo todos sus frutos y decirles "cuando estás escribiendo que las matemáticas no captan el elemento cualitativo, tu ordenador está traduciendo eso a una serie de ceros y unos. Imagínate lo que se puede hacer cuando hay más números". Y un último consejo. Acostúmbrate a pedir cifras que sustenten las afirmaciones. Cuando se afirma que "nuestro país es muy ineficiente implementando los programas públicos" o "el capitalismo ha multiplicado el número de pobres" exige que te den números como se hace en estas páginas web:
https://transitcosts.com/ https://www.usc.gal/economet/reviews/aeid1111.pdf https://ourworldindata.org/extreme-poverty
Por cierto, ambas afirmaciones son falsas...
Coda final
He dejado varios temas importantes fuera de estas notas, a saber, que las mates no santifican modelos sofisticados pero vacíos de sensatez, el papel de los modelos teóricos en el trabajo aplicado, la cruenta lucha que en los años 50 libraron partidarios y contrarios a usar bulldozers matemáticos en nuestras investigaciones, así como una explicación de los principales resultados de las ramas de nuestra disciplina que han usado matemáticas y como setenta y seis más... Pero como dijo un filósofo, eso son otras historias...
--------------------------------------------------------------------
[1]Deseo expresar mi agradecimiento a Salvador Barberá, Carmen Beviá, Antonio Cabrales, Félix Lobo, Ignacio Ortuño y Socorro Puy por sus consejos, que no siempre he seguido, pero que me han sido muy útiles en la elaboración de este trabajo. Todos los errores son míos.
[2]Parece que Smith (1776) copió punto por punto su ejemplo de los alfileres de la Enciclopedia de Diderot (1755)
Modelling the Pin Factory – The Origin of the Division of Labour Theory – Part 2
Otros autores que hablaron de la importancia de la división del trabajo incluyen a Turgot, Petty e Ibn-el-Khaldun un arábe de origen andalusí (1332-1406).
[3]Sin duda su ascendencia sefardita le sugirió poner a Portugal como más productiva que Inglaterra.
[4]A la vez que Menger y Walras...
[5]Responsable, entre otras cosas, de que los economistas escribamos los gráficos de oferta y demanda con los ejes cambiados...
[6]Sus condiciones, que aprendimos como Kuhn-Tucker, habían sido descubiertas 12 años antes por un matemático americano, Karush.
https://nadaesgratis.es/admin/de-como-la-candida-economia-se-entrego-a-las-matematicas-1
Parte II
https://nadaesgratis.es/luis_corchon/economia-y-matematicas-ii-de-como-shizuo-kakutani-salvo-a-adam-smith
"La respuesta de "sentido común" a la pregunta de .... ¿cómo se caracterizaría una economía motivada por la codicia y controlada por un gran número de agentes? sería, probablemente, el caos". Pero "hay una lista bastante impresionante de economistas, desde Adam Smith al presente, que han buscado probar que una economía descentralizada motivada por el auto interés y guiada por los precios es compatible con una disposición ordenada de los recursos económicos... y superior a una gran clase de sistemas alternativos"....
Arrow y Hahn, General Competitive Analysis. Holden Day, 1971 pp. vi y vii.
Arrow y Hanh
La oferta y la demanda en equilibrio parcial
La oferta y la demanda en equilibrio parcial es algo que todo el mundo entiende. Y mucha gente cree que sus propiedades son extrapolables a la economía en general y que con esto se puede entender cualquier problema económico. Spoiler. Pues no.
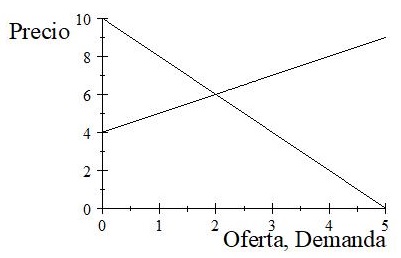
Todos somos familiares con el famoso gráfico.
Del que se sigue que existe un único equilibrio de mercado (con un precio de seis y dos unidades transaccionadas). Ese equilibrio es estable porque a un precio por encima de seis la oferta supera a la demanda y lo inverso ocurre cuando el precio es menor que seis. Además, movimientos de la oferta y la demanda tienen los efectos que la intuición sugiere.
El sistema en su conjunto
Si empezamos a pensar sobre el modelo anterior encontramos algunas cosas raras. Por ejemplo, ¿de dónde sale la renta con la que se compra ese bien? Y, si en el mundo hay una sola mercancía, ¿por qué se intercambia? Entonces comprendemos que, en realidad, el modelo anterior es una simplificación de un modelo en el que hay (por lo menos) dos mercancías. ¿Y qué pasa con el equilibrio en el mercado de la otra mercancía? Aquí viene en nuestra ayuda la ley de Walras que implica que, en un mundo con n mercados, si la oferta iguala a la demanda en n - 1 mercados, necesariamente el mercado restante está también en equilibrio.[2] Así que nuestro modelo anterior es un modelo de dos mercancías en el que el precio es el precio de esa mercancía relativo al de la otra mercancía (o relación de intercambio) y el equilibrio en ese mercado es suficiente para analizar el equilibrio de los dos mercados.
Haciendo alguna pirueta podemos interpretar el mercado de la figura como un mercado muy pequeño y el "otro mercado" como el resto de la economía. Pero el modelo anterior no es bueno si hay interacciones fuertes de ese mercado con otro, como en los mercados de energía o de alimentos. Y tampoco vale como una descripción del sistema económico porque la agregación de todos los demás mercados en uno es demasiada agregación. Resumiendo, el modelo de equilibrio parcial no es una buena guía para el análisis del sistema económico. Habremos de considerar modelos con más mercancías. Y eso hacemos.
Tres mercados... o más...
El bueno de Walras era consciente de que para analizar el sistema económico se necesitaban muchos mercados porque los sistemas económicos desde tiempos inmemoriales tienen muchísimas mercancías. Para ello amasó un porronazo de ecuaciones correspondientes a los mercados de bienes y de factores. Y las contó. Y como el número de precios relativos era igual al número de ecuaciones coligió que el sistema tenía, al menos, un equilibrio. Hoy casi cualquiera sabe que la igualdad entre el número de ecuaciones y el número de incógnitas no es ni condición necesaria ni suficiente de que un sistema de ecuaciones tenga una solución. Ejemplo, el sistema y = x + 3, x = y + 5 no tiene solución. ¿Qué podemos hacer?
Quiero remarcar que este problema no es una tecnicalidad. Si las ecuaciones que describen nuestro modelo de la economía no tienen solución, el modelo ES INCORRECTO. Y de él no puede extraerse conclusión válida alguna. Así, si suponemos que hay un número natural más grande que ninguno, llamémosle N, es fácil probar que tal número es uno (N ≥ N. N por hipótesis así que 0 ≥ N. (N-1) que implica N = 1 Tachannnnnn).
Ahora toca reflexionar ¿Por qué en el modelo de equilibrio parcial parece tan obvio que hay un equilibrio y que es único? Pues porque hemos pintado oferta y demanda astutamente de tal manera que para precios muy altos existe exceso de oferta y para precios bajos hay exceso de demanda. El teorema del valor intermedio nos garantiza que hay un precio para el que la oferta iguala a la demanda. Y ese teorema... ¿no vale en muchas dimensiones? Pues sí, pero no. Me explico.
El teorema del valor intermedio en n dimensiones se debe a Poincaré y Miranda y para nuestros nada siniestros propósitos puede enunciarse así:
Sean f1, f2, … fn funciones continuas de p1, p2, … pn cada una con rango en [0,1] y tales que, para todo i, cuando pi = 0, fi < 0 y cuando pi = 1, fi > 0.
Entonces hay unos p1, p2, …, pn tal que todas las fi = 0.
Interpretando los p como precios y las f como funciones de exceso de oferta, el teorema garantiza la existencia de unos precios tales que todos los mercados están en equilibrio. El problema son los supuestos.
La continuidad por ahora nos vale. Que el rango sea el intervalo cero uno es irrelevante. Cualquier otro intervalo (cerrado) nos serviría. Pero ¿por qué tiene que haber exceso de demanda de una mercancía cuando su precio es el mínimo sin importar cual sea el precio de los otros bienes? ¿Y si uno de esos precios es el salario de los consumidores de esa mercancía? En ese caso si ese salario es muy bajo la demanda de ese bien será cero. Y si esa mercancía no tiene utilidad alguna para sus poseedores estos la ofrecerán incluso si su precio es cero. En ese caso la función de oferta deja de ser univalorada (con un único valor en el rango para cualquier valor de los precios) para ser multivalorada. Glups! Y algunos de sus valores en el rango no cumplen los supuestos del teorema. Idénticas reflexiones se aplican a cuando el precio es el máximo. Pues puede ocurrir que los precios de los factores con los que se produce ese bien también sean máximos y sea imposible producir ese bien a beneficio no negativo.
Aún más canalla es el siguiente ejemplo:
Supongamos que existen una mercancía y un consumidor tales que ese consumidor tiene recursos iniciales sólo de esa mercancía, le gusta esa mercancía, pero no está interesado en el consumo de ninguna otra mercancía. Y hay otros consumidores que tienen recursos iniciales de esa mercancía, pero no están interesados en su consumo. Entonces no existe un equilibrio.
Prueba: Sea x la demanda de esa mercancía por parte de ese consumidor, w sus recursos iniciales de esa mercancía y W la oferta total de esa mercancía, mayor que w por hipótesis. Supongamos que hay un precio para el que ese mercado está en equilibrio p. Entonces la restricción presupuestaria de ese consumidor es px = pw. Nótese que p > 0 porque si no, ese consumidor demandaría cantidades arbitrariamente grandes de esa mercancía. Luego dividiendo la restricción presupuestaria por p, tenemos que x = w < W contradiciendo que el mercado está en equilibrio.
El ejemplo es, extremo, pero debe alertarnos para que no supongamos sin más que el equilibrio de mercado existe.
La solución... en el próximo capítulo...
[1]Agradezco a Carmen Beviá, Juan D. Moreno-Ternero y Jaume Sempere sus comentarios a una versión preliminar de este trabajo. Soy el único responsable de las opiniones aquí vertidas.
[2]La ley de Walras se prueba sumando las restricciones presupuestarias de todos los consumidores.
Economía y matemáticas (III). De cómo Shizuo Kakutani salvó a Adam Smith*
Un estudiante alto y atlético esperaba nervioso a la puerta del despacho de -nada más y nada menos- uno de los grandes genios del siglo XX, John von Neumann. En su mano llevaba unas hojas que podían significar un cambio radical en el estudio de la economía y en su carrera. El paseo de unos treinta minutos entre la universidad de Princeton y el Instituto de Estudios Avanzados se le había hecho muy corto[1]. Solo había salido de su ensimismamiento cuando pasó por delante de la casa de Einstein. La visión de los magníficos campos de golf que tanto solía gustarle no le entretuvo ni medio minuto. Se estaba jugando su futuro (y el de la microeconomía). Y aquí conviene pausar el relato.
La microeconomía en 1949
Por no andar con rodeos, la microeconomía en 1949 era un fracaso. Aparte del modelo de oferta y demanda en un solo mercado poco se había avanzado en temas cruciales como:
● El equilibrio de varios mercados. El bueno de Walras había llenado un libraco muy gordo con ecuaciones y ecuaciones, pero poco se sabía de si tales ecuaciones tenían una solución, o sea de si el modelo era mínimamente consistente y mucho menos de las propiedades de tales ecuaciones.
● Situaciones estratégicas en las que las acciones de los agentes se influyen mutuamente. El llamado "problema del oligopolio" era un fantasma con el que se asustaba convincentemente a cualquiera que se atreviera a asomarse a ese campo.
● Como consecuencia de lo anterior nuestro conocimiento de áreas importantes como el oligopolio, el riesgo y la incertidumbre, los conflictos, la información asimétrica, la negociación, los impuestos óptimos, los contratos, las votaciones, etc. era rudimentario por decir algo.
● No había conexión con las otras ciencias sociales. La historia, la ciencia política, la psicología y la sociología eran icebergs lejanos y aparentemente inaccesibles.
Estos temas, así como los esfuerzos en los últimos 70 años para rellenar esos socavones de nuestro conocimiento ya los he tratado en una entrada anterior a la que remito al lector para una primera visión de la economía moderna. Lo remarco para que ningún alma crítica, cándida y bienpensante tenga la ocurrencia de identificar la economía de hoy con la llamada "economía neoclásica". Y retomamos el hilo anterior.
John Forbes Nash llama a la puerta
Nuestro nervioso estudiante por fin encuentra valor para golpear suavemente la puerta del despacho del gran genio. Unos angustiosos segundos de espera y la voz esperada le da permiso.[2] Allí delante hay un hombre pequeño de aspecto vulgar con chaqueta y corbata que parece estar domando algo, con un lápiz como batuta, que se intenta escapar de sus papeles. Le indica con un movimiento de la mano que tome asiento. Y cambiando de actividad, ahora parece buscar algo en uno de los cajones de su mesa, le insta a hablar. Nash comienza a contarle su cosita dejando bien claro que se trata de una extensión de un trabajo del genio de hace 21 años. El genio, sigue que te sigue buscando algo que se le resiste, asiente dando a entender que una (pequeña) parte de su cerebro ha localizado este tema: el equilibrio de un juego de dos personas y de suma cero, un resultado mono, pero, dados sus supuestos, casi irrelevante. Nash lanza la bomba. "Tengo una generalización de ese resultado para cualquier número de jugadores y juegos de suma arbitraria". El genio continúa como si nada. Y Nash empieza la parte más técnica de su contribución (ver acá). Entonces von Neumann masculla suavemente. "Ah claro es un punto fijo". Nash asiente, le da las gracias al genio y sale de su despacho visiblemente conmocionado. Un año más tarde su trabajo se publica en los Proceedings of the National Academy of Sciences of the United States of America, una muy prestigiosa revista. Aún es un estudiante de doctorado. Unos años más tarde Arrow, Debreu y McKenzie (entre otros) basándose en el resultado de Nash consiguen probar la existencia del equilibrio perfectamente competitivo. Así en cinco años se desatascan temas -los puntos 1 y 2 de la lista anterior- que llevaban atormentando a la profesión décadas y décadas. Y en medio se crean la elección social (Arrow), la economía axiomática y la teoría de la negociación (Nash otra vez). Las generaciones posteriores pueden dedicarse a desarrollar esta sólida base (puntos 3 y 4)[3].
Ah se me olvidaba. El instrumento matemático que usa Nash[4], vamos, el desatascador, había sido publicado en 1941 por Shizuo Kakutani un matemático japonés que habiendo pasado por el Instituto de Estudios Avanzados había tratado con von Neumann.[5] Después de la guerra volvió al Instituto y luego a Yale. Su hija Michiko tenía la reputación de ser una de las críticas literarias más fieras del New York Times. Y también es autora.
Todo este lío ¿para qué?
Seamos sinceros. Las matemáticas no tienen buena prensa en este país. Y no voy a intentar arreglar eso ahora. Una de las quejas que uno oye a menudo a los estudiantes de grado de economía y similares es que están ahí para entender la sociedad no para ser abrumados con toneladas de matemáticas. Y que no ven la necesidad de todo aquello. Así que queridos apabullados, os lo voy a explicar.
La prueba de la existencia de que nuestro modelo preferido tiene un equilibrio es básica porque sin ella no existirían regularidades a estudiar. Y nuestra creencia de que en sistemas económicos descentralizados existe un equilibrio y por tanto unas regularidades no estaría justificada. Si el resultado de ese sistema fuera el caos, posiblemente el estudio de esos sistemas no tendría sentido ya que los datos no dirían nada[6]. Desde un punto de vista lógico la existencia de equilibrio es una comprobación de que el modelo no posee contradicciones internas en las relaciones que postula[7].
Pero hay más. La economía trata de sistemas muy complejos. Vais a ver. Imaginemos el siguiente modelo:
Variable x ↑ Variable y ↓ Variable z
donde ↑ significa que la variable de la izquierda determina la variable de la derecha y que la relación es creciente, eso es a mayores valores de x le siguen mayores valores de y. ↓ significa lo mismo, pero ahora la relación es decreciente o sea a mayores valores de y le siguen menores valores de z. Supongamos que hay un aumento de x. Sabemos por nuestro esquema que eso llevará a un aumento de y y una disminución de z. No necesitamos ninguna fórmula abtrusa que nos diga cómo funciona ese modelo. Por ejemplo, una subvención (x) aumenta la electricidad producida (y) y disminuye el precio de esta (z). Pero si esa disminución del precio hace que la recaudación sea menor, eso disminuye la subvención y la producción y aumenta el precio, lo cual nos lleva a.... La simple interacción entre z y x hace que no podamos decir que efecto tendrá una subvención en el precio de la electricidad... Qué decir si el sistema tuviera unas interacciones aún complejas. A veces veo diagramas con flechas volando hacia todas partes y me pregunto qué se puede aprender de eso...
Resumiendo, que es gerundio
La microeconomía trata de sistemas complejos que podemos representar por modelos en los que la mayoría de las variables están interrelacionadas. Un modelo de una economía sin sector exterior ni gobierno mínimamente realista debería tener, al menos tres tipos de consumidores (jóvenes, adultos y retirados), tres tipos de bienes de consumo -agrícolas, industriales y servicios- tres inputs además del trabajo -energía, capital fijo y primeras materias- tres tipos de trabajadores -clasificados por sus niveles educativos- y tres activos financieros -bonos, acciones y depósitos bancarios. Pregunta: ¿Qué efecto tendrá sobre los precios agrícolas un pequeño incremento de la productividad de los trabajadores más educados? Inténtalo sin un modelo matemático. Y luego mira a ver si descifras lo que pasa en el resto de la economía. Como dice Dani Rodrik, necesitamos las matemáticas porque no somos suficientemente listos igual que necesitamos grúas porque no somos suficientemente fuertes...
Y si te repugna la visión de que lo que hacen los mercados es resolver ecuaciones, piensa que cuando estás montando una bici, tu cerebro está resolviendo unas muy complicadas ecuaciones diferenciales.
[*] Los comentarios de Carmen Beviá, Juan Luis Jiménez, Lourdes Moreno y Juan D. Moreno-Ternero han ayudado notablemente a perfilar los argumentos aquí expuestos. Todos los errores y omisiones son de mi exclusiva responsabilidad.
[1] Una fuente de informaciones interesantes sobre el Instituto es esta.
[2] El aspecto y la voz en inglés del genio pueden verse y escucharse aquí
[3] El libro de Sylvia Nasar "A Beautiful Mind" es una referencia obligada para la vida de Nash.
[4] Sugerido por David Gale otro destacadísimo matemático y economista de la misma hornada que Nash que junto con el laureado Lloyd Shapley -también de esa hornada- inventó los modelos de emparejamiento. Nash, Gale y Shapley hicieron la tesis con Albert Tucker que formalizó el dilema del prisionero y que junto a Harold Kuhn (otro Pricetoniano) desarrolló las condiciones de optimización que nos son tan familiares a los economistas.
[5] Kakutani era consciente de la aplicación de su resultado a la teoría de juegos, pero se conformó con una nueva prueba del teorema de von Neumann, ver esto.
[6] Pero no todo estaría perdido, ver la investigación de este señor antiguo alumno de licenciatura de la Complutense.
[7] El modelo puede ser autocontradictorio si sus conceptos básicos no están bien ensamblados. Una tonelada de matemáticas avanzadas no convierte a un modelo en lógicamente invulnerable.





No hay comentarios:
Publicar un comentario