Un experimento online de Teoría de Juegos: Envidia y solidaridad
Por Pablo Brañas-Garza
(@BehSnaps) con Alfonso Robles, Carmen Hidalgo, Esteban Marquez,
Guillermo Molina, Humberto Franco, Ignacio Perez, Jaime Gómez, Javier
Pino, Javier Sánchez, Jimena Moreno, Luis Alcala, María Alonso, Maria
Neira, Marta París, Miguel Villar, Miguel Fernández, Roberto Mengibar,
Valeria Herrera y Vicente Moreno.
El pasado 28 de octubre hicimos un experimento “online” desde la clase de Microeconomía III: Teoría de Juegos de la Universidad Loyola en Sevilla (@LoyolaAnd, @LoyolaEcon). El objetivo del experimento era “enseñar” a los estudiantes si el modelo de preferencias “sociales” de Fehr-Schmidt (1999) funcionaba en la vida real. En este modelo los individuos se preocupan por los pagos – las ganancias- de los demás de manera benevolente (solidaridad) o no (envidia). Como segundo objetivo, además de lo anterior, lanzamos dos tratamientos: un dilema de presos con normal (estrategias: Cooperar y No Cooperar) y otro sin framing (estrategias: A o B).
Para estudiar tanto la envidia/solidaridad como la cooperación en un dilema de presos lanzamos un experimento online a través de WhatsApp. En la entrada de hoy nos centraremos en la envidia y la solidaridad.
El modelo de Fehr-Schmidt
Este modelo incorpora preferencias sociales a la función de utilidad tradicional. Concretamente, la utilidad se ve afectada por la envidia – lo que nos molesta que otros tengan más que nosotros- y la solidaridad – lo que nos molestan que otros tengan menos:
Instrucciones
Se utilizó Google Forms para poner las instrucciones del experimento. Todos los sujetos fueron dirigidos a una de las dos webs (control y tratamiento) alojadas en esta plataforma. El mensaje de invitación era el mismo, sólo cambiaba el link.
La web tenía dos partes. En la primera había: a) una introducción general al experimento; b) consentimiento informado; c) solicitud del número de teléfono (para llamarle si era premiado) y consentimiento para guardarlo; d) quién le había invitado.
En la segunda parte preguntábamos: a) sexo; b) universidad; c) las preguntas sobre envidia y solidaridad (ver Figura 1); d) la decisión sobre cooperar o no; e) las expectativas de cooperación del rival y f) si quería ser llamado para otros experimentos.
En las instrucciones, con toda claridad, se decía que 10 personas serían elegidas al azar para pagarles en función de sus decisiones en el dilema de presos (donde podían ganar 0, 1, 5 o 10 euros).

Teníamos dos problemas a resolver: llegar al mayor número de personas posible y que la asignación al tratamiento no dependiera del alumno – es decir, evitar que todos los amigos de un estudiante fueran al mismo tratamiento. Para salvar los dos escollos a la vez se usó el siguiente procedimiento.
Todos los alumnos crearon 4 grupos de difusión en su WhatsApp: G1, G2, G3 y G4. Cada alumno metió sus primeros 25 contactos en G1, los siguientes 25 en G2, los siguientes en G3, luego en G4, los siguientes de nuevo en G1, luego en G2, etc. Es decir, cada paquete de 25 iba entrando en orden en G1, G2, G3, G4, G1, G2, G3, G4, etc. Cada alumno informó del número de sujetos que tenía en cada grupo G, es decir, su aportación de contactos al experimento. Es importante resaltar que para minimizar la attrition (invitados que deciden no participar) los alumnos no mandaron mensajes a grupos sino a contactos personales.
A cada alumno, de manera aleatoriamente, se le sorteó una regla de asignación (C es grupo de control, T es tratamiento): CCTT, TTCC, CTCT o TCTC. Es decir, el alumno que recibió TCTC tuvo que mandar a sus contactos de G1 y G3 a la web del tratamiento y a los contactos de G2 y G4 al control.
Lo anterior nos permite conocer la “semilla” de aleatorización, es decir, saber a qué grupo T o C se asignó aleatoriamente cada contacto. La suma de la cantidad de contactos en ambos grupos nos da el número de mensajes enviados.
A las 12:20 de la mañana se lanzaron los 2358 mensajes por WhatsApp.
-
https://nadaesgratis.es/admin/un-experimento-online-de-teoria-de-juegos-envidia-y-solidaridad
El pasado 28 de octubre hicimos un experimento “online” desde la clase de Microeconomía III: Teoría de Juegos de la Universidad Loyola en Sevilla (@LoyolaAnd, @LoyolaEcon). El objetivo del experimento era “enseñar” a los estudiantes si el modelo de preferencias “sociales” de Fehr-Schmidt (1999) funcionaba en la vida real. En este modelo los individuos se preocupan por los pagos – las ganancias- de los demás de manera benevolente (solidaridad) o no (envidia). Como segundo objetivo, además de lo anterior, lanzamos dos tratamientos: un dilema de presos con normal (estrategias: Cooperar y No Cooperar) y otro sin framing (estrategias: A o B).
Para estudiar tanto la envidia/solidaridad como la cooperación en un dilema de presos lanzamos un experimento online a través de WhatsApp. En la entrada de hoy nos centraremos en la envidia y la solidaridad.
El modelo de Fehr-Schmidt
Este modelo incorpora preferencias sociales a la función de utilidad tradicional. Concretamente, la utilidad se ve afectada por la envidia – lo que nos molesta que otros tengan más que nosotros- y la solidaridad – lo que nos molestan que otros tengan menos:
U(X,Y) = X - A x MAX [Y-X, 0] - B x MAX [X-Y, 0],
donde X es la ganancia propia e Y la de la otra persona. El término A
captura la envidia que sufrimos porque el otro gana más que yo (se
activa cuando Y>X y se multiplica por ese valor) y B es la pena
causada por que el otro gana menos (se activa cuando X>Y). Siguiendo a
Cabrales y Ponti (2011), destacamos cuatro grupos de parámetros de especial interés.
“Egoístas”: A = B = 0. Los sujetos tienen
preferencias “tradicionales”, es decir no les preocupa ni la envidia ni
la solidaridad.
“Aversos a la desigualdad”: 0 ≤ B < 1,
B ≤ A. Los sujetos son tanto envidiosos como solidarios pero lo primero
es más importante que lo segundo.
“Buscadores de estatus”: 0 ≤ A < 1,
-1 < B ≤ 0, siendo el valor absoluto de B menor o igual que el de
A: |B| ≤ |A|. En este caso, los individuos son también envidiosos, pero
además “disfrutan” de que existan otros con peores resultados que ellos.
“Buscadores de eficiencia”: -0,5 ≤ A <
0, 0 < B ≤ 0,5, siendo el valor absoluto de A menor o igual que el
de B: |A| ≤ |B|.este caso, los individuos sufren por los que están peor,
pero disfrutan de que haya otros con mejores resultados que ellos.
A lo largo de este experimento estudiaremos si la envidia y la
solidaridad realmente importan. Dicho de otro, si en el mundo real hay
gente que se comporta acorde a los tipos recientemente mencionados.Instrucciones
Se utilizó Google Forms para poner las instrucciones del experimento. Todos los sujetos fueron dirigidos a una de las dos webs (control y tratamiento) alojadas en esta plataforma. El mensaje de invitación era el mismo, sólo cambiaba el link.
La web tenía dos partes. En la primera había: a) una introducción general al experimento; b) consentimiento informado; c) solicitud del número de teléfono (para llamarle si era premiado) y consentimiento para guardarlo; d) quién le había invitado.
En la segunda parte preguntábamos: a) sexo; b) universidad; c) las preguntas sobre envidia y solidaridad (ver Figura 1); d) la decisión sobre cooperar o no; e) las expectativas de cooperación del rival y f) si quería ser llamado para otros experimentos.
En las instrucciones, con toda claridad, se decía que 10 personas serían elegidas al azar para pagarles en función de sus decisiones en el dilema de presos (donde podían ganar 0, 1, 5 o 10 euros).

Figura 1
Envío de mensajes y aleatorizaciónTeníamos dos problemas a resolver: llegar al mayor número de personas posible y que la asignación al tratamiento no dependiera del alumno – es decir, evitar que todos los amigos de un estudiante fueran al mismo tratamiento. Para salvar los dos escollos a la vez se usó el siguiente procedimiento.
Todos los alumnos crearon 4 grupos de difusión en su WhatsApp: G1, G2, G3 y G4. Cada alumno metió sus primeros 25 contactos en G1, los siguientes 25 en G2, los siguientes en G3, luego en G4, los siguientes de nuevo en G1, luego en G2, etc. Es decir, cada paquete de 25 iba entrando en orden en G1, G2, G3, G4, G1, G2, G3, G4, etc. Cada alumno informó del número de sujetos que tenía en cada grupo G, es decir, su aportación de contactos al experimento. Es importante resaltar que para minimizar la attrition (invitados que deciden no participar) los alumnos no mandaron mensajes a grupos sino a contactos personales.
A cada alumno, de manera aleatoriamente, se le sorteó una regla de asignación (C es grupo de control, T es tratamiento): CCTT, TTCC, CTCT o TCTC. Es decir, el alumno que recibió TCTC tuvo que mandar a sus contactos de G1 y G3 a la web del tratamiento y a los contactos de G2 y G4 al control.
Lo anterior nos permite conocer la “semilla” de aleatorización, es decir, saber a qué grupo T o C se asignó aleatoriamente cada contacto. La suma de la cantidad de contactos en ambos grupos nos da el número de mensajes enviados.
A las 12:20 de la mañana se lanzaron los 2358 mensajes por WhatsApp.
Inmediatamente después, un estudiante no europeo mandó la invitación a
dos grupos enormes de Erasmus (162 y 257 personas). Por error se
mandaron los dos al Control, en vez de mandar uno de ellos al
Tratamiento. Otra chica de la clase mandó el Tratamiento a un grupo de
64 personas. En suma, se mandaron 483 mensajes mas.
En total se mandaron 1576 mensajes al Control (cooperar/no) incluyendo los 419 de los grupos y 1265 al Tratamiento (A/B).
A los 12:45 teníamos 300 participantes, a las 13:00 ya había 400, a
las 13:40 eran 700 y a las 17:10 pasamos de mil. El experimento se cerró
a las 11:49 noche con 1172 respuestas, de las cuáles 45 habían jugado
dos veces. Es decir, se logró obtener respuestas de 1127 individuos
diferentes.
El día 29 a las 00:00 se extrajeron 10 participantes, se emparejaron
entre ellos y se les calculó el pago. Se les informó a las 9:00 y se les
pagó por Bizum.
¿Funcionó? Balance entre tratamientos
En la Tabla 1 mostramos los resultados básicos del balance. Se puede
apreciar que en el grupo de control se recibieron 634 respuestas de
individuos diferentes (56% del total de respuestas recibidas), mientras
que el grupo de tratamiento 493 (44%). No encontramos diferencias entre
control y tratamiento en sexo, envidia y solidaridad. Tampoco se
encuentran diferencias entre ambos grupos en la disposición de
participar en futuros experimentos. Y sobre todo, no encontramos
diferencias en la attrition.
Tabla 1: Prueba de balance
En resumen, no encontramos ninguna diferencia significativa (p>0,1). Todo lo anterior implica que la aleatorización funcionó bien.
La envidia, la solidaridad y el modelo de Fehr-Schmidt
En la Figura 2 mostramos el histograma de la envidia. Recordad que es
auto-reportada y sin incentivos (ver Figura 1). Lo más llamativo es que
la moda está a la izquierda: la mayoría de los participantes dicen que
no son envidiosos, de hecho, el 65% dice ser muy poco envidioso (niveles
de preocupación 1, 2 y 3). Si miramos por género, encontramos que las
mujeres no son distintas de los hombres (p=0,53).
Figura 2: Envidia
La solidaridad aparece en la Figura 3. Como en el caso anterior la
solidaridad es auto-reportada y sin incentivos. En esta ocasión, la moda
está centrada y aparecen distintos valores con cierta popularidad a lo
largo del espacio de respuestas. En este caso si encontramos que las
mujeres dicen ser más solidarias que los hombres (p=0.00).
Figura 3: Solidaridad
Para terminar, miremos lo uno y lo otro conjuntamente para cada
individuo. Para tener un visión directa dividiremos las dos variables en
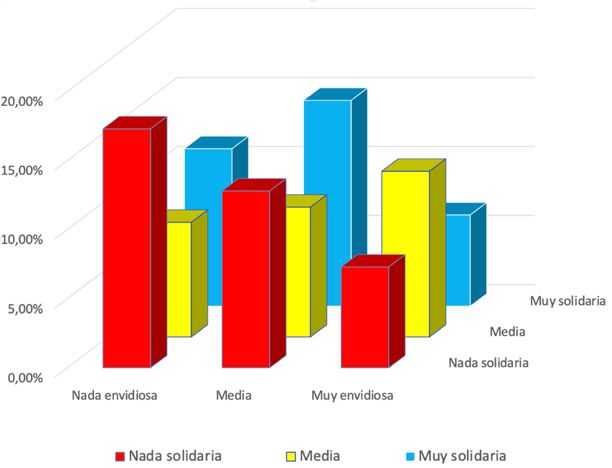
terciles y haremos una tabla de doble entrada. La Figura 4 muestra
dichos datos de manera gráfica. La solidaridad aparece de atrás hacia
delante: rojo es nada solidario y azul es muy solidario. La envidia va
de izquierda a derecha (izquierda nada envidioso y derecha muy
envidioso). Los datos están en la Tabla 1.
Figura 4: Envidia y solidaridad
De este gráfico destacaremos lo siguiente. Lo primero y más llamativo
es la enorme heterogeneidad. ¡Hay gente de todo tipo! El grupo más
numeroso está adelante a la izquierda (17,3%), es decir, personas que
dicen que no le importan ni la envidia ni la solidaridad. Estos sujetos
son precisamente “racionales”, aquellos que funcionan con una función de
utilidad tradicional, esto es, sin preferencias sociales (no tienen ni
envidia ni solidaridad).
También son un grupo bastante numeroso los del fondo (azul) en el
medio (14,9%), esto es, dicen ser muy solidarios y reconocen tener un
nivel medio de envidia. A la derecha del grupo de los racionales está
un grupo de “casi” racionales (12,8%), puesto que dicen ser nada
solidarios y un poco envidiosos. Curiosamente el grupo con menor
representación son los muy solidarios y muy envidiosos (6,6%).
En muy destacable que los resultados son bastante similares a Cabrales et al.
(2010). En cualquier caso, creo que el mensaje más importante es la
heterogeneidad. No podemos concluir que ahí fuera hay un solo tipo de
individuos sino que más bien hay de todo en la viña del Señor.
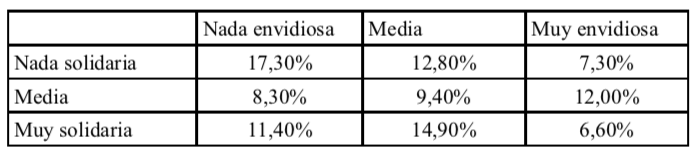
Tabla 2: Envidia y solidaridad
Resumen
En resumen, es razonablemente sencillo hacer experimentos con rigor y
seriedad desde el aula usando algo tan sencillo como el WhatsApp.
Experimentos que los alumnos disfrutan enormemente y que les sirven para
aprender conceptos, a veces, demasiado abstractos. Hay que tener en
cuenta que Google Forms permite hacer un seguimiento online de
las respuestas. En nuestro caso estuvimos dos horas de clase viendo y
comentando resultados en tiempo real.
Hay dos cosas más que quiero añadir. Para realizar este experimento
no hay que tener laboratorio, ni programar, ni siquiera tener un
servidor. Google Forms lo hace para nosotros. Por último, el
coste de este experimento ha sido bastante moderado. Los pagos de los 10
ganadores sumaron 42 euros.
Pablo Brañas-Garza, Loyola Behavioral LAB y sus alumnos de la Universidad Loyola-
https://nadaesgratis.es/admin/un-experimento-online-de-teoria-de-juegos-envidia-y-solidaridad



No hay comentarios:
Publicar un comentario